Parte 2: Gráficas velocidad vs tiempo – Ejemplo 2

Objetivos
Terminada la lección podrás:
- Resolver problemas de cinemática.
- Calcular el desplazamiento.
Parte 2: Gráficas velocidad vs tiempo – Ejemplo 2
Ejemplo #2
Veamos otro ejemplo en el que un tren se mueve a una velocidad constante de 40m/s. Queremos calcular el desplazamiento total del tren durante los primeros 50 segundos. Observa que a medida que el tiempo transcurre la posición del tren va cambiando. La siguiente imagen muestra la posición del tren durante los primeros 6 segundos.
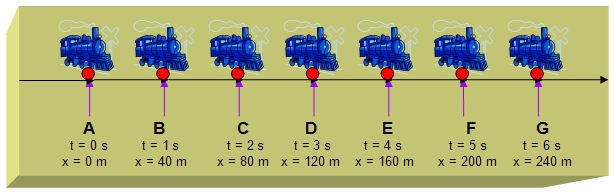
Cambio de posición
El tren cambia de posición aumentando su desplazamiento. Cuando comienza su desplazamiento justo en ese punto es cero, porque arbitrariamente tomamos ese punto como el inicio de nuestra gráfica y le asignamos valores de (0m, 0s). Sin embargo, en ese punto hay velocidad, el objeto se está moviendo en todo momento, ni acelera ni desacelera. Esto significa que aunque la posición sea 0 y el tiempo es 0 cuando un objeto se mueve con rapidez o velocidad constante o uniforme no se detiene en ese punto, se va desplazando. Su distancia cambia, siempre aumenta pero su desplazamiento depende de la posición y dirección de ese movimiento.
Tiempo de movimiento
En la vida real un tren puede moverse durante un periodo de tiempo mayor. Algo interesante sería aumentar el tiempo hasta 60 segundos o un minuto. Podemos hacer una tabla con los datos. Esta vez lo haremos usando incrementos de 10 segundos en vez de 1 segundo para demostrar lo que ocurre con la posición del tren luego de transcurridos 60 segundos o un minuto de tiempo. Recuerda que el problema que tratamos de resolver requiere analizar la situación hasta 50 segundos solamente.
Tabla de datos
Al igual que en matemáticas, cuando construimos una tabla de datos tratamos de tener la mínima cantidad de puntos que nos permita representar mejor la situación. En este caso aumentamos hasta 60 segundos porque quisimos hacerlo pero no es requisito que siempre lo hagas. todo depende de la situación que debas analizar.
Para facilitar nuestro análisis escribiremos en la tabla de datos lo que sabemos hasta el momento. Es decir, si el tren se mueve a una velocidad constante tendría una velocidad de 40m/s desde el comienzo o tiempo igual a cero y a medida que el tiempo transcurre cada 10 segundos. En 20, 30, 40 , 50 y 60 segundos se movería con una velocidad de 40m/s. Veamos la siguiente tabla de datos que recoge esas ideas:
| Punto | Tiempo (s) | Velocidad (m/s) |
| A | 0 | 40 |
| B | 10 | 40 |
| C | 20 | 40 |
| D | 30 | 40 |
| E | 40 | 40 |
| F | 50 | 40 |
| G | 60 | 40 |
Ahora veamos la gráfica dibujada usando esos datos:
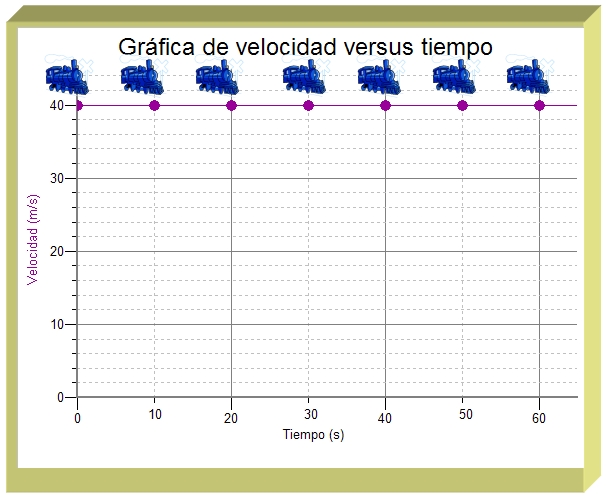
Observa la imagen que muestra al tren en cada uno de los puntos. Lo que significa que el tren posee una misma velocidad. La gráfica tiene una forma lineal horizontal a través de todo el recorrido. Como en el ejemplo anterior podemos calcular el desplazamiento buscando el área bajo la curva.
Gráfica del movimiento
Veamos la siguiente gráfica en la que solamente consideraremos lo que ocurre hasta un tiempo igual a 50 segundos:
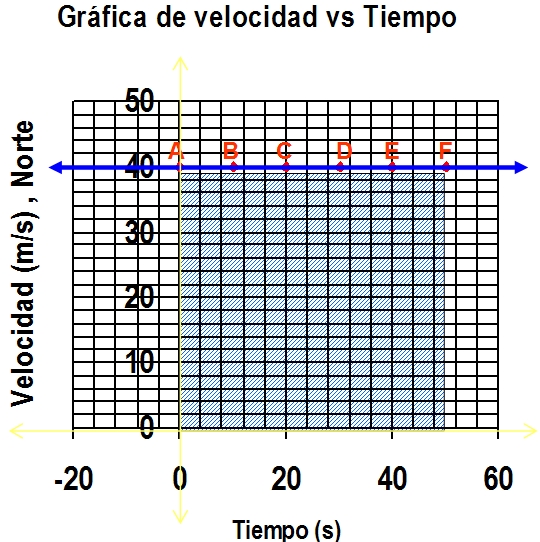
Vemos marcados en la gráfica los puntos A, B, C, D, E y F. Estos puntos muestran la posición del tren en ese periodo de tiempo de 50 segundos y a la vez podemos apreciar el rectángulo que determina el área bajo la curva.
Cálculos y ecuación
Debemos determinar la diferencia del origen en la velocidad y la diferencia en en el tiempo lo cual podemos calcular usando la siguiente ecuación:
- Desplazamiento = D
- Área=A
- Largo= L
- ancho=a
- Cambio = (diferencia entre cantidades)
- A = L x a = V x t = D
En otras palabras el desplazamiento (D) es la multiplicación de la diferencia entre la velocidad desde el origen y la diferencia en el tiempo desde el origen para este ejemplo. Si el tiempo inicial fuese 10s entonces el cambio en el tiempo o la diferencia en tiempo sería 50s – 10s = 40s.
Área bajo la curva
En este ejercicio simplificamos la solución porque comenzamos en el origen. El área bajo la curva de una gráfica de velocidad versus tiempo es el desplazamiento. Observemos la siguiente gráfica:
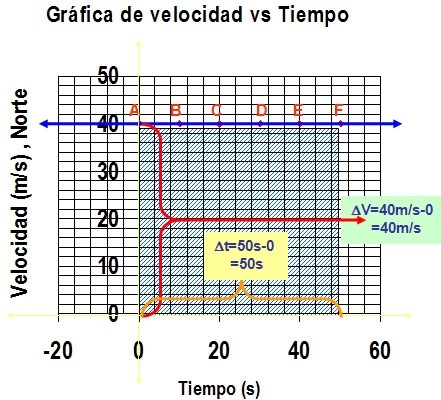
Cálculos
Para calcular el desplazamiento en el tramo de A hasta F solo debemos considerar lo siguiente:
- A = L x a
- V x t = D
El desplazamiento es V x t = D donde la V es 40m/s – 0 = 40m/s y el t es 50s-0 = 50s. Ahora colocamos todo en la ecuación de
D= V x t = (40m/s-0) x (50s – 0s)=
D= 40m/s X 50 s
Desplazamiento=D= 2,000 m, Norte
Si queremos el desplazamiento individual de cada tramo lo podemos calcular de igual forma calcula así:
- 1-D = 40m/s x (10 s – 0s) = 40m/s x 10 s = 400 m, Norte
- 2-D = 40m/s x (20 s – 10s) = 40m/s x 10 s = 400 m, Norte
- 3-D = 40m/s x (30 s – 20s) = 40m/s x 10 s = 400 m, Norte
- 4-D = 40m/s x (40 s – 30s) = 40m/s x 10 s = 400 m, Norte
- 5-D = 40m/s x (50 s – 40s) = 40m/s x 10 s = 400 m, Norte
Si sumamos todos los desplazamientos individuales obtenemos el siguiente resultado que es igual a la respuesta anterior:
Total D= 2,000 m, Norte
Tabla de datos
La siguiente tabla organiza los resultados y muestra las respuestas a cada una de las cantidades de tramo, forma de la gráfica, velocidad, tiempo y desplazamiento según calculadas y expresadas aquí:
| Tramo | Forma de la gráfica | Velocidad (m/s) | Tiempo (s) | Desplazamiento (m) | Desplazamiento total (m) |
| AB | Lineal Horizontal | Constante en 40m/s, N | Aumenta de 0 a 10 | 400 m,N | 400 m,N |
| BC | Lineal Horizontal | Constante en 40m/s, N | Aumenta de 10 a 20 | 400 m,N | 800 m,N |
| CD | Lineal Horizontal | Constante en 40m/s, N | Aumenta de 20 a 30 | 400 m,N | 1,200 m,N |
| DE | Lineal Horizontal | Constante en 40m/s, N | Aumenta de 30 a 40 | 400 m,N | 1,600 m,N |
| EF | Lineal Horizontal | Constante en 40m/s, N | Aumenta de 40 a 50 | 400 m,N | 2,000 m,N |
Observa que las columnas de desplazamiento y desplazamiento total son diferentes ya que en el desplazamiento solamente indicas cuanto se desplazó en ese tramo pero en el desplazamiento total debes sumar las cantidades tomando en consideración la dirección Norte o Sur de acuerdo a la situación demostrada.
En resumen:
- Hay que hacer una distinción entre lo que es distancia y lo que es desplazamiento.
- Definitivamente son diferentes. ¿Puedes diferenciarlas?
- La distancia se mide en términos del valor absoluto desde el punto de comienzo hasta el punto final.
- El desplazamiento tiene dirección y se suman o restan las cantidades que dependen de la dirección. Se le asigna un signo a esa dirección para poder establecer la posición para obtener un valor, así como, la dirección en el resultado final.
Ejercicios de práctica:
Problema de práctica 1:
Considera un camión que se mueve a lo largo de una línea recta a una velocidad uniforme de 50m/s por 40 s, se detiene y luego vira en la dirección que venía, moviéndose a una velocidad uniforme de 80m/s por un periodo de 30s. La siguiente tabla contiene los datos del movimiento de un camión.
1. Haz un diagrama para demostrar el movimiento del camión y dibuja la gráfica.
| Punto | Tiempo (s) | Velocidad (m/s) |
| A | 0 | 0 |
| B | 10 | 0 |
| C | 10 | 50 |
| 20 | 50 | |
| 30 | 50 | |
| 40 | 50 | |
| D | 50 | 50 |
| E | 50 | 0 |
| 60 | 0 | |
| F | 70 | 0 |
| G | 70 | -80 |
| 80 | -80 | |
| 90 | -80 | |
| H | 100 | -80 |
| I | 100 | 0 |
2. Determina la forma de la gráfica, la velocidad, el desplazamiento y el desplazamiento total según puedas determinarlo en cada tramo. Para esto llena la tabla de datos que aparece a continuación.
| Tramo | Forma: | Velocidad (m/s) | Tiempo (s) | Desplazamiento (m) | Desplazamiento Total (m) |
| AB | |||||
| BC | |||||
| CD | |||||
| DE | |||||
| EF | |||||
| FG | |||||
| GH | |||||
| HI |
3. Puedes ver la tabla de datos y la gráfica para analizarla aquí abajo:
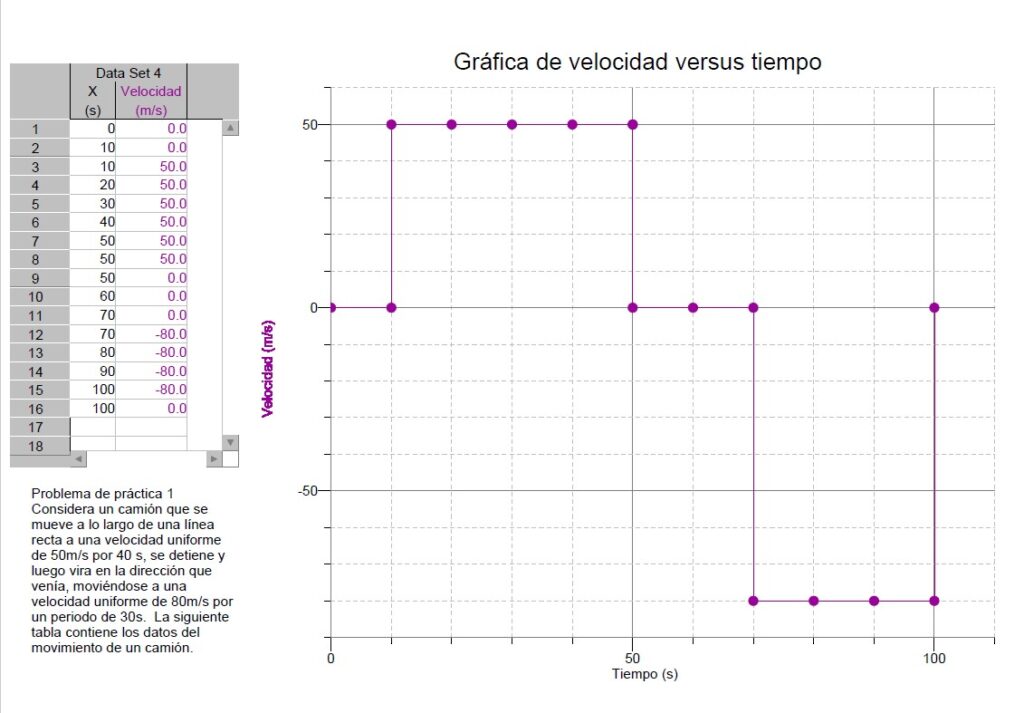
4. Revisa tu respuesta en el enlace Parte 7: Problemas de velocidad vs tiempo – Soluciones. En estas páginas podrás tener la respuesta de los ejercicios de práctica e información adicional que te permitirá entender mejor el tema usando los recursos de este pequeño tutorial del curso de Física en línea.
Páginas asociadas a este tutorial:
<<Continuar con la Parte 3: Problemas de Práctica 2 & 3 para gráficas de velocidad vs tiempo >>
- 1 Parte 1: Gráficas de velocidad vs tiempo
- 2 Parte 2: Gráficas de velocidad vs tiempo Ejemplo 2
- 3 Parte 3: Problemas de Práctica 2 & 3 para gráficas de velocidad vs tiempo
- 4 Parte 4: Gráficas de velocidad vs tiempo – Ejemplo 3: Aceleración
- 5 Parte 5: Gráfica de velocidad vs tiempo – Problema de práctica 4
- 6 Parte 6: Gráfica de velocidad vs tiempo – Problemas de práctica 5
- 7 Parte 7: Problemas de velocidad vs tiempo Soluciones
Presentación
Enlaces externos para explorar
- Conceptos de Física: Hyperphysics
- Libros:
- NASA: Science Explorer Poster Series
- Simulaciones: PhET
- Tutorial de Física en Inglés: Physics Classroom
- Wikipedia en Español: Wikipedia
Simulación
Vídeo
Movimiento
Páginas recientes
- Carl Friedrich Gauss: Matemática y Física
- La IA Revoluciona la Investigación
- Ernest Rutherford y su Legado
- Antoine Henri Becquerel y la Radiactividad
- La Ocultación en Astronomía
- Escribiendo el Póster de la Investigación
- Presentando la Investigación – Poster
- Movimiento de Traslación en el Universo
- Movimiento de Rotación en el Universo
- Webquest: Explorando el Universo
- Metodo, Procedimiento e Investigación
- Maria Skłodowska-Curie y la Radiactividad
- Investigando el Desplazamiento de Wien
- El Hielo, la Nieve y la Lluvia Helada
- Niels Bohr y la Estructura Atómica
Más páginas para explorar
-

¡Vistiendo para el Espacio!
-

Abstract: Resumen Breve de Investigación
-

Aceleración en Caída Libre
-

Aceleración Grativacional en Planetas
-

Aceleración Gravitacional en la Tierra
-

Aceleración Lineal y sus Representaciones
-

Aisladores y Conductores
-

Alacena virtual de conversiones
-
Albert Einstein Historia y Vida
-
Alessandro Volta y la Electricidad
-

Amedeo Avogadro y su Ley
-
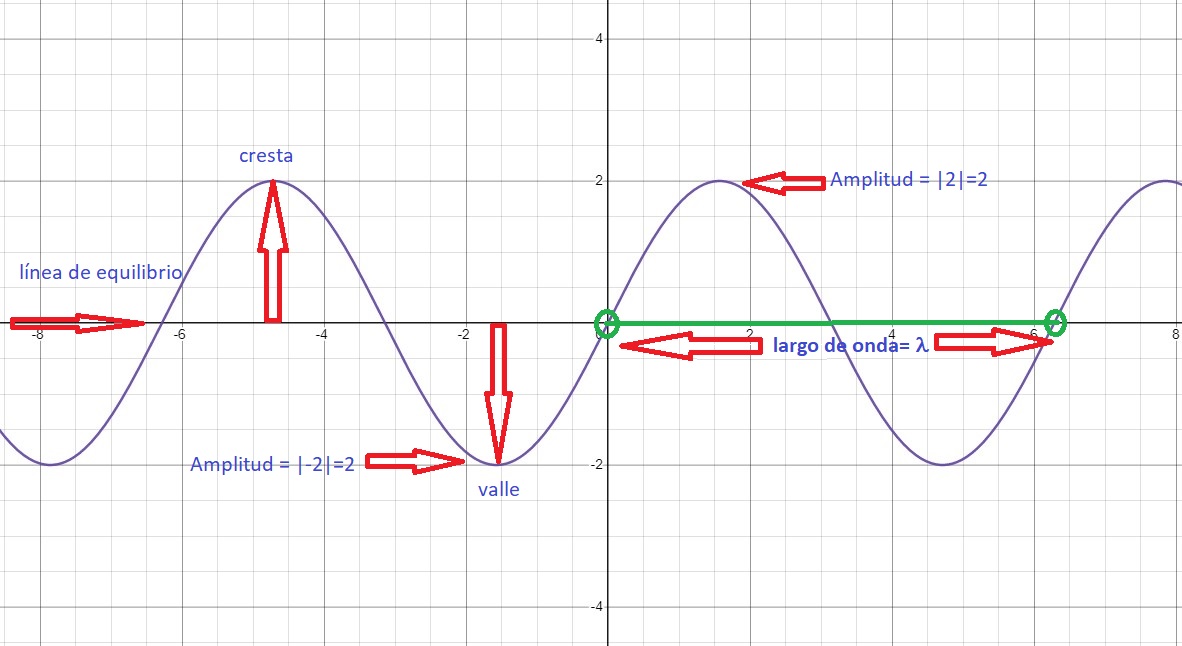
Amplitud, largo de onda y frecuencia
-

Análisis Gráfico del Movimiento
-

Andrés Ampere y el Electromagnetismo
-

Antoine Henri Becquerel y la Radiactividad
-

Ernest Rutherford y su Legado
-

Antoine Henri Becquerel y la Radiactividad
-
La Ocultación en Astronomía
-
Herramientas para el Análisis Gráfico

Para que una gráfica sea útil, esta debe ser dibujada adecuadamente. Las gráficas permiten una visualización inmediata de los datos.
-
Los Estados de la Materia
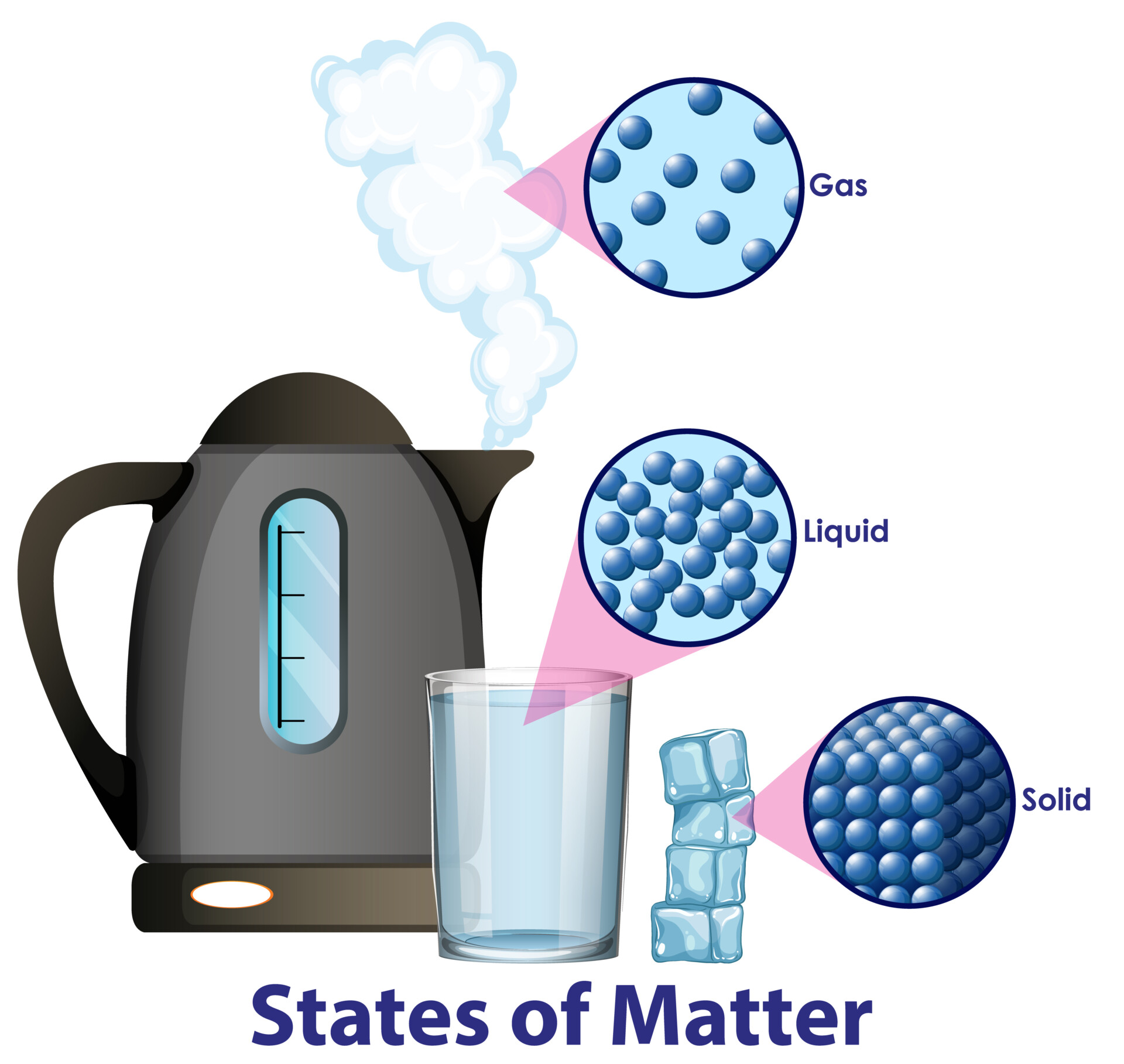
Los estados de la materia son formas de la materia en el universo. Se distinguen porque sus partículas constituyentes (átomos, moléculas o iones) se agrupan.
-
Compara Balanzas: Análoga o Digital
La balanza es una palanca de primer grado que tiene dos brazos de igual tamaño, Mediante el equilibrio entre los pesos de dos cuerpos comparas sus masas.













