Objetivos:
Al terminar esta la lección:
- Definirás las funciones trigonométricas a partir de la geometría del triángulo rectángulo.
- Explicarás como medir los ángulos de un triángulo.
- Utilizarás las funciones trigonométricas para hallar las medidas desconocidas de un triángulo rectángulo.
- Seleccionarás correctamente la función trigonométrica apropiada para resolver los problemas.
La Trigonometría
La trigonometría es una rama de las matemáticas que se dedica al estudio de las relaciones entre los lados y los ángulos de los triángulos. 1 En esencia, nos permite analizar y calcular medidas de triángulos, lo cual es fundamental en muchas áreas de la ciencia y la ingeniería.
¿Por qué es importante la trigonometría?
- Geometría: Es esencial para resolver problemas geométricos que involucran triángulos y círculos.
- Física: Se utiliza en campos como la mecánica, la óptica y la electricidad para analizar movimientos, fuerzas y ondas.
- Ingeniería: Es fundamental en el diseño de estructuras, puentes, edificios y maquinaria.
- Astronomía: Se emplea para calcular distancias y posiciones de estrellas y planetas.
- Navegación: Se utiliza en la navegación marítima y aérea para determinar posiciones y rutas.
- Gráficos por computadora: Se aplica en la creación de imágenes y animaciones 3D.
Conceptos clave en trigonometría:
- Triángulo rectángulo: Un triángulo que tiene un ángulo recto (90 grados).
- Hipotenusa: El lado opuesto al ángulo recto en un triángulo rectángulo.
- Catetos: Los otros dos lados de un triángulo rectángulo.
- Funciones trigonométricas: Seno, coseno, tangente, cotangente, secante y cosecante. Estas funciones relacionan los lados de un triángulo rectángulo con sus ángulos.
Los ángulos
Un ángulo se define como el resultado de la intersección de dos rayos. Los rayos que componen el ángulo se denominan lados, mientras que el unto de intersección se denomina vértice.
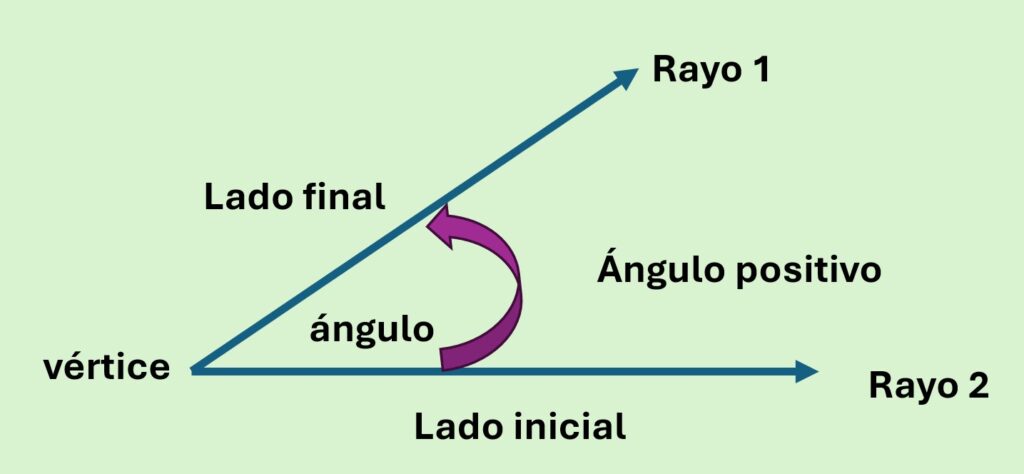
Los triángulos rectángulos
Los triángulos son figuras geométricas con tres lados y tres ángulos. Existen varios tipos de triángulos, entre ellos el triángulo rectángulo. Este tipo de triángulo se caracteriza por tener uno de sus ángulos con medida igual a 90°. A este ángulo también se le conoce como ángulo recto. La suma de todos los ángulos en un triángulo es de 180°. En el caso de los triángulos rectángulos, como el ángulo recto mide 90°, entonces los otros dos ángulos sumados son igual a 90°.
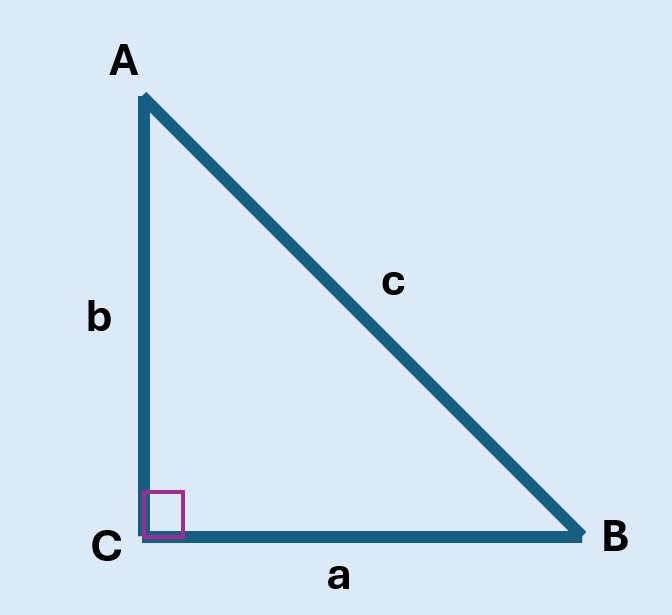
Triángulo con Vértice C
Sea el triángulo ACB un triángulo rectángulo con el ángulo recto en el vértice C. Sus lados a y b son sus catetos y el lado c la hipotenusa. Cada ángulo, en el triángulo tiene un lado opuesto, lado de frente al ángulo, y un lado adyacente, lado que forma parte del ángulo en cuestión.
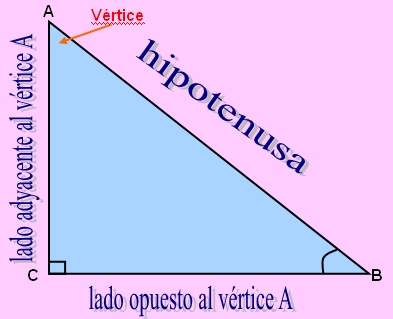
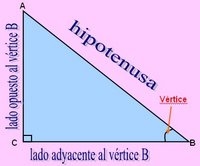
El vértice
De la forma en que ha sido configurado el triángulo en este ejemplo, el vértice A tiene al cateto a como lado opuesto y al cateto b como lado adyacente. De igual forma el vértice B tiene al cateto b como lado opuesto y al cateto a como lado adyacente. Los lados opuestos y adyacentes se intercambian entre sí para los dos ángulos que no son el ángulo recto en el triángulo rectángulo.
En el caso del ángulo recto, hay que notar que tiene como lado opuesto a la hipotenusa y no tiene lado adyacente. El identificar los lados opuestos y adyacentes respecto a un ángulo es sumamente importante a la hora de definir las funciones trigonométricas.
Funciones Trigonométricas Básicas
En esta unidad solamente definiremos las tres funciones trigonométricas básicas: seno, coseno y tangente. Estas son:
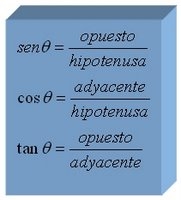
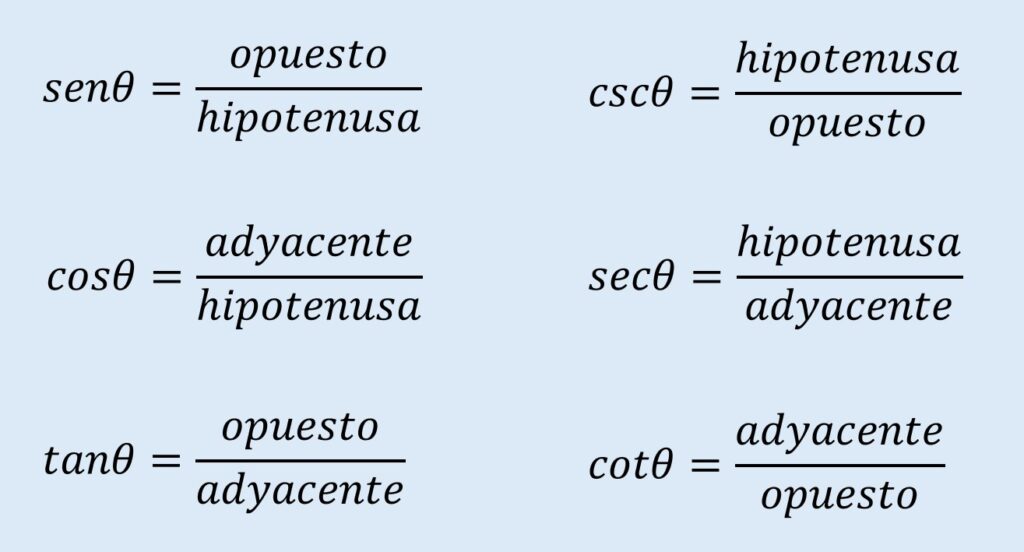
Existen otras funciones trigonométicas como sec θ, csc θ y cot θ. Estas se pueden definir en términos de las funciones principales de sen θ, cos θ y tan θ. Por esta razón en Física se trata de usar las cantidades fundamentales y es más conveniente utilizarlas para resolver problemas.
¿Qué puedes hacer con la trigonometría?
- Calcular lados desconocidos de un triángulo: Si conoces algunos lados y ángulos, puedes encontrar los demás utilizando las funciones trigonométricas.
- Determinar ángulos desconocidos: Si conoces los lados de un triángulo, puedes calcular sus ángulos.
- Resolver problemas de altura y distancia: La trigonometría se utiliza para calcular alturas de edificios, distancias entre puntos y otros problemas similares.
- Modelar fenómenos periódicos: Muchos fenómenos naturales, como las ondas sonoras y las mareas, tienen un comportamiento periódico que puede ser modelado utilizando funciones trigonométricas.
En resumen
La trigonometría es una herramienta poderosa que te permite analizar y calcular medidas en una amplia variedad de situaciones. Desde la construcción de edificios hasta el estudio del universo, la trigonometría desempeña un papel fundamental.
Presentación
Simulación
Vector Addition
Enlaces externos para explorar
- Conceptos de Física: Hyperphysics
- Libros:
- NASA: Science Explorer Poster Series
- Simulaciones: PhET
- Tutorial de Física en Inglés: Physics Classroom
- Wikipedia en Español: Wikipedia
Vídeo
Trigonometría Básica
Funciones trigonométricas
Páginas recientes
- Pirotecnia y los Fuegos Artificiales
- La Inteligencia Artificial y la Física
- Constelación de Orión: El Cazador
- Mecánica Clásica y Análisis Gráfico
- Herramientas Para Medir la Masa
- Extremófilos: Increíbles Adaptaciones
- Fuerza Boyante: Así Flotamos
- La Física y las Gráficas de Velocidad
- El Péndulo Simple: Un Clásico de la Física
- Fuerza de Tension Superficial
- Burbujas de Jabón Esféricas
- Resistencia del Aire: Freno Invisible
- Práctica Interactiva de Medidas
- Trigonometría: Un Mundo de Ángulos
- Sumar y Restar con Cifras Significativas
-
Herramientas Para Medir la Masa
La balanza es una palanca de primer grado que tiene dos brazos de igual tamaño, Mediante el equilibrio entre los pesos de dos cuerpos comparas sus masas.
-
Trigonometría: Un Mundo de Ángulos
La trigonometría es una rama de las matemáticas que se dedica al estudio de las relaciones entre los lados y los ángulos de los triángulos.
-
Sumar y Restar con Cifras Significativas
Los dígitos significativos aportan información real sobre la precisión de una medida. Nos indican qué tan confiables son los números que estamos utilizando.