
Objetivos:
Al terminar la lección podrás:
- Explicar los conceptos: momentum, impulso y ley de conservación de momentum.
- Ofrecer ejemplos de momentum y su conservación.
Conservación del momentum:
La ley de conservación del momentum establece que el momento inicial de un sistema es igual al momento final de ese sistema.
El principio de conservación del momentum establece que, en un sistema aislado (sin fuerzas externas), el momentum total antes y después de una interacción, como una colisión, se mantiene constante. Esto significa que el momentum de los objetos puede cambiar, pero la cantidad total de momentum en el sistema no varía.
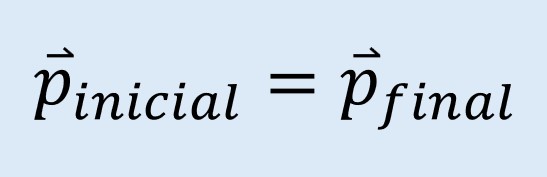
Esto es válido tanto para colisiones elásticas (donde no se pierde energía) y los objetos continúan en movimiento luego de la colisión. También aplica en las inelásticas (donde se pierde algo de energía) porque los objetos se unen y siguen juntos el movimiento luego de la colisión.
Tipos de colisiones:
Colisión elástica:
En una colisión elástica, tanto el momentum como la energía cinética total se conservan. Esto significa que los objetos rebotan sin perder energía en forma de calor, deformaciones u otros efectos.
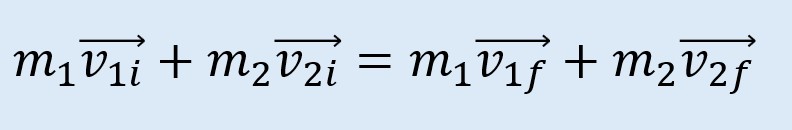
Donde:
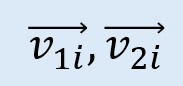
Las velocidades iniciales de los objetos antes de la colisión se expresan como:
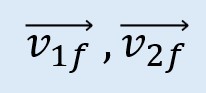
son las velocidades finales después de la colisión.
Colisión inelástica:
En una colisión inelástica, el momentum se conserva, pero parte de la energía cinética se pierde debido a deformaciones, calor o sonido. En los casos más extremos, los objetos pueden quedarse pegados y moverse juntos después de la colisión.
Este tipo de colisión completamente inelástica require que los objetos queden juntos después de la colisión, y su velocidad común final puede calcularse usando ecuaciones y aplicando el principio de conservación del momentum:
Volvemos a la siguiente ecuación que fue con la que comenzamos:
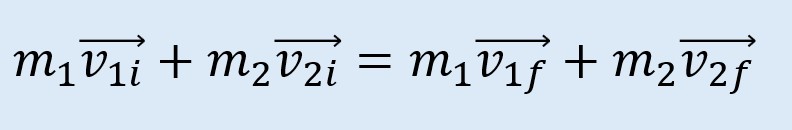
Sustitución de datos y consideraciones en la ecuación:
Consideramos que luego de la colisión de los objetos las velocidades finales se igualan:
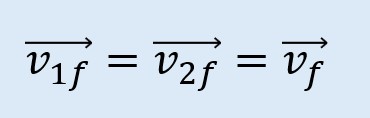
Entonces consideramos lo que sucede con las masas al final:
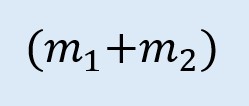
Se convierten en una sola masa de esta forma:
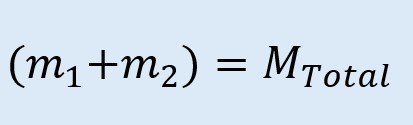
Sustituyendo en la ecuación inicial:
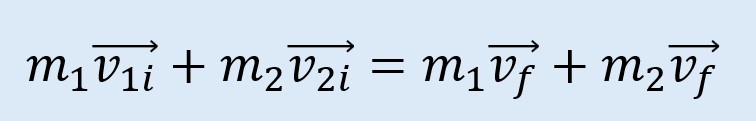
Entonces la velocidad final es un factor común y redistribuimos:
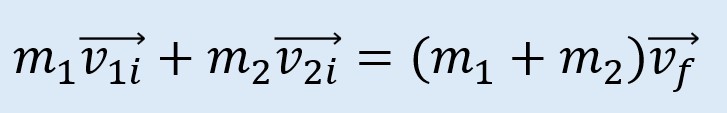
Conisderando la suma de las masas entonces:
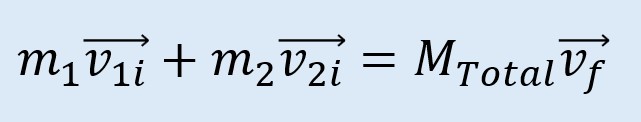
Al final obtenemos:
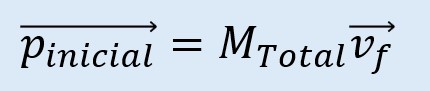
Vemos como la velocidad final es común después de la colisión y lo que importa es la masa total del sistema.
Ejemplos de momentum y colisiones:
- Pelota de fútbol: Cuando un jugador patea una pelota de fútbol, le transfiere momentum. Cuanto más rápido y más masivo sea el pie del jugador y la velocidad con la que patea, mayor será el momentum que adquiere la pelota.
- Colisión de coches: En un choque entre dos vehículos, el momentum de ambos vehículos antes del impacto se distribuye de acuerdo con sus masas y velocidades. Aunque la energía puede perderse en forma de sonido, calor y deformación, el momentum total del sistema se conserva.
- Rebote de una pelota de tenis: Cuando una pelota de tenis rebota en el suelo, su momentum cambia de dirección, pero el cambio está relacionado con la fuerza que el suelo ejerce sobre ella. En cada rebote, parte de la energía se disipa, por lo que cada vez rebota a una altura menor.
Impacto del momentum en la vida cotidiana:
El concepto de momentum se encuentra en muchos aspectos de la vida cotidiana. Desde el movimiento de vehículos, hasta deportes, e incluso en las interacciones de objetos en el espacio. Por ejemplo, los ingenieros utilizan el principio de conservación del momentum para diseñar sistemas de seguridad en colisiones de vehículos y para calcular los efectos del impacto en accidentes.
Resumen:
El momentum es una medida de la cantidad de movimiento de un objeto y se define como el producto de su masa por su velocidad. Es una cantidad conservada en los sistemas aislados, lo que significa que el momentum total antes y después de una colisión permanece constante. Las colisiones pueden ser elásticas, donde se conserva la energía cinética, o inelásticas, donde parte de la energía se convierte en otras formas. El concepto de momentum es fundamental en la física clásica y tiene amplias aplicaciones en el estudio del movimiento y las interacciones entre objetos.
Enlaces externos para explorar
- Telescopios en vivo: Hubble y Webb
- Simulaciones: PhET
- Conceptos de Física: Hyperphysics
- Tutorial de Física en Inglés: Physics Classroom
Simulaciones
Péndulo de Newton
Choque de partículas
Esta simulación te ayudará a comprender el momento de inercia
Vídeo
Explicación sencilla
Colisiones elásticas y las inelásticas
Momentum lineal
Páginas recientes
- Carl Friedrich Gauss: Matemática y Física

- La IA Revoluciona la Investigación

- Ernest Rutherford y su Legado

- Antoine Henri Becquerel y la Radiactividad

- La Ocultación en Astronomía

- Escribiendo el Póster de la Investigación

- Presentando la Investigación – Poster

- Movimiento de Traslación en el Universo

- Movimiento de Rotación en el Universo

- Webquest: Explorando el Universo

- Metodo, Procedimiento e Investigación

- Maria Skłodowska-Curie y la Radiactividad
- Investigando el Desplazamiento de Wien

- El Hielo, la Nieve y la Lluvia Helada

- Niels Bohr y la Estructura Atómica
Exploremos un poco más
-

Solución de Problemas Posición vs Tiempo
-

Incertidumbre y Sistema de Mediciones
-

Balanza y Escalas: Mide la Masa
-
Definición de Física en Línea
-

Introducción a Física en Línea
-

Ejemplo Usando Estrategias
-

Física una ciencia matemática, páginas y recursos
-

Ejemplo Dígitos Significativos
-

Cifras Significativas y Estimadas
-

Reglas de los dígitos significativos
-
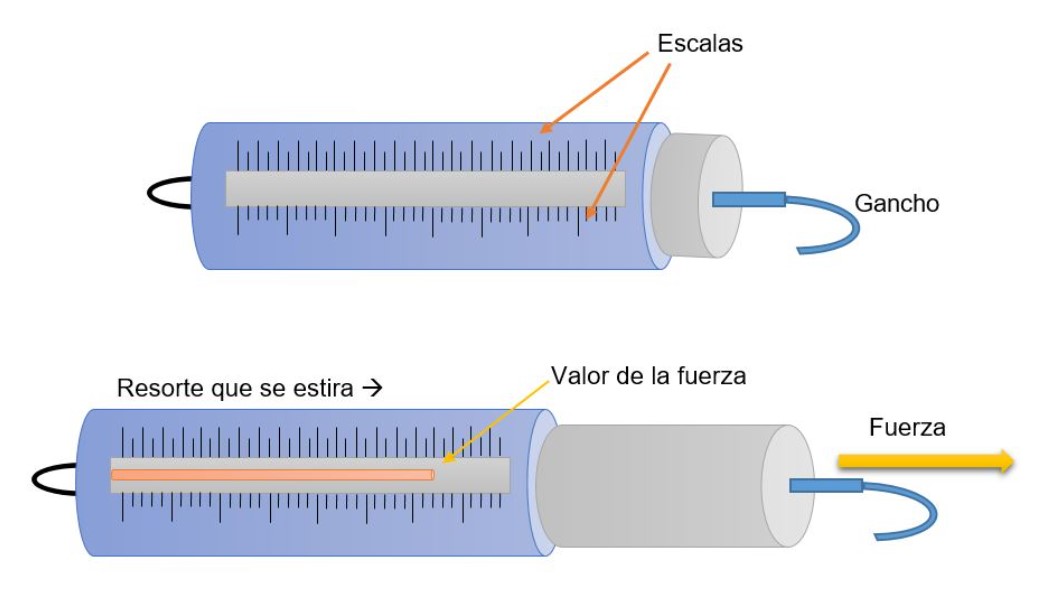
Dinamómetro y su Escala
-

Unidades Fundamentales en Ciencia
-
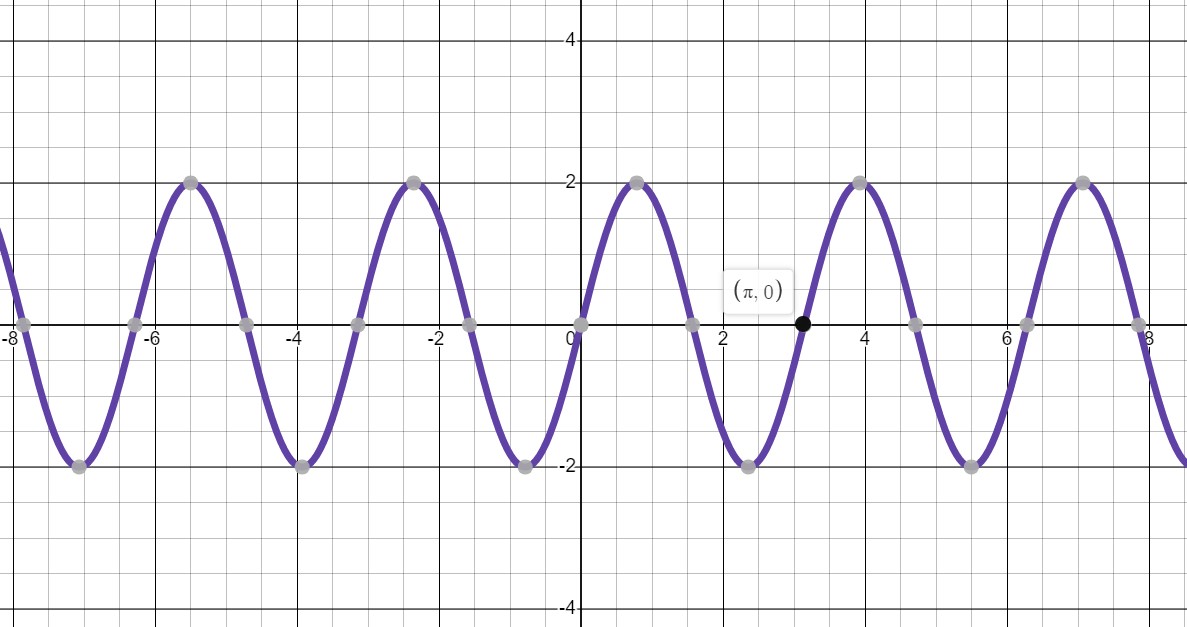
Introducción a las ondas
-

Errores Sistemáticos y Porciento de Error
-

CERN es para la Investigación Nuclear
-

Ernest Rutherford y su Legado
-

Antoine Henri Becquerel y la Radiactividad
-
La Ocultación en Astronomía
