Momento Angular: Relación con el Torque

Las palancas usan el torque o la fuerza efectiva para hacer rotar un objeto. Por James Hayward en Pexels en: https://www.pexels.com/photo/close-up-of-details-in-the-machine-structure-17126404/

Objetivos:

Terminada la lección podrás:

Explicar los conceptos fundamentales del momento angular y el torque.

Elba M Sepulveda

Momento Angular y su Relación con el Torque

Introducción

En el vasto universo de la física, el movimiento no se limita a traslaciones lineales; los objetos también giran y rotan. Para describir y comprender estos movimientos rotacionales, la física introduce conceptos clave como el momento angular y el torque. Mientras que el momento lineal es fundamental para describir el movimiento en línea recta, el momento angular se erige como su análogo rotacional, proporcionando una poderosa herramienta para analizar sistemas que giran. La íntima relación entre el momento angular y el torque es la piedra angular para entender cómo las fuerzas aplicadas provocan cambios en la rotación de un objeto.

¿Qué es el Momento Angular?

El momento angular (L) es una magnitud física que describe la cantidad de movimiento de rotación de un objeto. Es el análogo rotacional del momento lineal (p=mv) en el movimiento de traslación.

Para una partícula de masa m que se mueve con velocidad v en una trayectoria circular de radio r, el momento angular se define como:

L=r×p=r×(mv)

Donde r es el vector de posición desde el origen al punto donde se encuentra la partícula, y p es el momento lineal de la partícula. Es importante destacar que el momento angular es una cantidad vectorial, lo que significa que tiene magnitud y dirección. La dirección del momento angular se determina por la regla de la mano derecha.

Para un objeto extenso que gira (como un disco o una esfera), el momento angular se define como:

L=Iω

Donde:

I es el momento de inercia del objeto, que es una medida de su resistencia a cambiar su estado de rotación (análogo a la masa en el movimiento lineal). Depende de la distribución de la masa del objeto y del eje de rotación.
ω es la velocidad angular del objeto, que es la velocidad con la que gira (medida en radianes por segundo).

La unidad del momento angular en el Sistema Internacional (SI) es el joule-segundo (J·s) o kilogramo-metro cuadrado por segundo (kg·m²/s).

¿Cómo se relaciona el Momento Angular con el Torque?

La relación entre el momento angular y el torque es análoga a la relación entre el momento lineal y la fuerza en el movimiento lineal.

El torque (τ) (también conocido como momento de fuerza) es la capacidad de una fuerza para producir una rotación o un cambio en el estado de rotación de un objeto. Es el análogo rotacional de la fuerza.

La relación fundamental es:

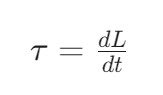
Ecuación de torque igual al cambio del momento angular sobre el tiempo.

Esta ecuación establece que el torque neto que actúa sobre un objeto es igual a la tasa de cambio de su momento angular con respecto al tiempo.

En otras palabras:

Si no hay torque neto actuando sobre un sistema (τ=0), el momento angular del sistema se mantiene constante. Esto se conoce como el Principio de Conservación del Momento Angular.
Si hay un torque neto aplicado, el momento angular del sistema cambiará. Un torque positivo aumentará el momento angular (aceleración angular), y un torque negativo lo disminuirá (desaceleración angular).

La unidad del torque en el Sistema Internacional (SI) es el newton-metro (N·m).

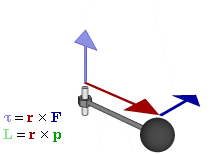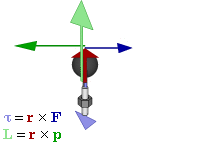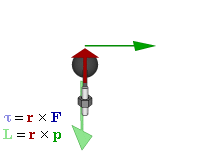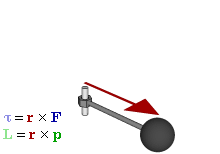
Animación de torque y momento angular. En Wikipedia, https://es.wikipedia.org/wiki/Momento_de_fuerza#/media/Archivo:Torque_animation.gif

Ejemplos

1. Conservación del Momento Angular

Patinadora sobre hielo: Una patinadora que gira con los brazos extendidos tiene un cierto momento de inercia grande y una velocidad angular relativamente baja. Cuando la patinadora acerca sus brazos al cuerpo, su momento de inercia disminuye drásticamente. Para conservar su momento angular (ya que el torque externo neto es despreciable), su velocidad angular debe aumentar, haciendo que gire mucho más rápido. (Li=Lf⇒Iiωi=Ifωf)
Tuffadores/Clavadistas: Un clavadista que salta de un trampolín y se encoge en el aire (posición de ovillo) reduce su momento de inercia, lo que le permite girar más rápidamente para realizar varias vueltas. Al extenderse antes de entrar al agua, su momento de inercia aumenta, y su velocidad angular disminuye, permitiendo una entrada suave.
Planetas y Estrellas: En un sistema solar, los planetas que orbitan una estrella. La fuerza gravitatoria ejercida por la estrella sobre el planeta apunta aproximadamente hacia el centro de masa de la estrella, lo que resulta en un torque neto cercano a cero (en un sistema ideal). Por lo tanto, el momento angular de cada planeta alrededor de la estrella se conserva, lo que explica por qué los planetas se mueven más rápido cuando están más cerca de la estrella (menor r, mayor v para conservar L=mvr).

2. Cambio en el Momento Angular debido al Torque

Acelerar una rueda de bicicleta: Para que una rueda de bicicleta en reposo comience a girar, se le debe aplicar un torque (por ejemplo, pedaleando). Este torque provoca un cambio en el momento angular de la rueda, llevándola de cero a un valor determinado. Si se aplica un freno, este ejerce un torque opuesto, reduciendo el momento angular de la rueda hasta detenerla.
Abrir una puerta: Al empujar el pomo de una puerta (ejerciendo una fuerza a una distancia del eje de rotación de las bisagras), se aplica un torque a la puerta. Este torque cambia el momento angular de la puerta, haciéndola girar y abrirse. Si la puerta ya se está abriendo y se aplica una fuerza para detenerla, se ejerce un torque opuesto, reduciendo su momento angular.
El giro de un giroscopio: Un giroscopio que gira tiene un momento angular significativo. Si se le aplica un pequeño torque externo (por ejemplo, la gravedad si no está equilibrado), en lugar de simplemente caer, el giroscopio experimenta un fenómeno llamado precesión, donde su eje de rotación gira lentamente alrededor de una dirección. Este comportamiento es una manifestación de cómo el torque cambia la dirección del momento angular.

Conclusión

El momento angular y el torque son conceptos interconectados y esenciales para comprender el comportamiento de los sistemas en rotación. El momento angular cuantifica la “cantidad de rotación” de un objeto, mientras que el torque es la causa de los cambios en esa rotación. La relación fundamental que establece que el torque neto es la tasa de cambio del momento angular es una de las leyes más potentes de la física, que rige desde el movimiento de los planetas hasta el funcionamiento de una lavadora.

La conservación del momento angular, en ausencia de torques externos, es un principio de belleza y utilidad inmensas, evidenciando la profunda simetría en las leyes de la naturaleza. Comprender estos conceptos no solo enriquece nuestra visión del mundo físico, sino que también proporciona las herramientas para diseñar y analizar una miríada de tecnologías rotatorias que son fundamentales en la vida moderna.