
Objetivos
Al terminar la lección:
- Definirás las funciones trigonométricas a partir de la geometría del triángulo rectángulo.
- Explicarás como medir los ángulos de un triángulo.
- Utilizarás las funciones trigonométricas para hallar las medidas desconocidas de un triángulo.
- Seleccionarás correctamente la función trigonométrica apropiada para resolver los problemas.
Relación de tres igualdades
La ley de seno es una relación de tres igualdades que siempre se cumplen entre los lados y ángulos de un triángulo cualquiera. En ocasiones necesitarás resolver ejercicios que envuelven triángulos que no son rectángulos. La ley del seno y la del coseno son muy convenientes para resolver problemas de triángulos en los que no hay ningún ángulo recto, es decir es para triángulo que no son rectágulos como los discutidos en la sección de trigonometría básica.
Prueba de la ley de seno
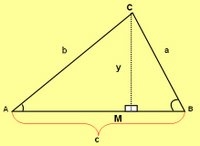
Veamos el triángulo de la derecha. Para obtener la ley de seno podemos realizar el siguiente procedimiento:
| Procedimiento | Resultado |
|---|---|
| En el triángulo ΔAMC aplicamos el seno del ángulo A y utilizamos la propiedad de la igualdad para obtener: | sen A = y/by/b = sen A |
| Ahora despejamos para y, obtenemos | y= b sen A |
| En el triángulo ΔBMC aplicamos el seno del ángulo B, utilizamos la propiedad de la igualdad y obtenemos | sen B = y/ay/a = sen B |
| De igual modo espejamos para y, obtenemos | y= a sen B |
| Igualamos ambas expresiones y = y de forma que: | b sen A = a sen B |
Entonces:
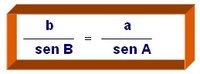
La ley del seno nos dice que la razón entre la longitud de cada lado y el seno del ángulo opuesto a el en todo triángulo es constante.
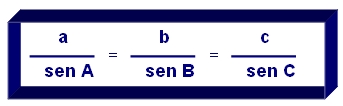
La ley del seno se escribirá como sigue:
Ejemplo 1: Medida del triángulo
Encuentra la medida del lado b para el triángulo ABC según demostrado en la siguiente figura:
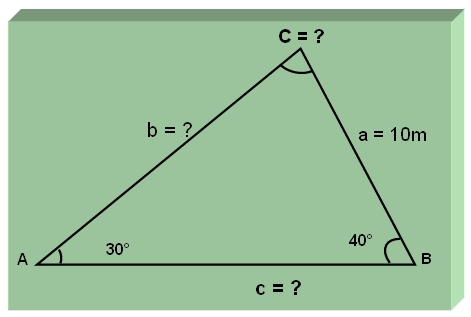
Estrategias para resolver el ejercicio:
Primero determina los datos:
- lado, a=10m
- ángulo, A=30°
- ángulo, B =40°
- lado desconocido, b = ?
Luego utiliza o aplica la siguiente ecuación:

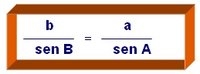
Despeja para la desconocida b y se sustituyen los valores:


Una vez realizados los cáculos mátemáticos podemos decir qe la respuesta es que la medida del lado b es de aproximadamente 13m. Usamos el redondeo a dos cifras significativas.
Algunas ideas importantes al resolver ejercicios de trigonometría
- Reemplaza los valores conocidos en la ley del seno.
- Usa una calculadora o una tabla trigonométrica para ir desde el seno de A hasta obtener la medida del ángulo A según demostrado.
- Ofrece el resultado en oración completa.
Práctica adicional
Encuentra la medida del ángulo C y del lado c para el triángulo ABC según demostrado en la figura:
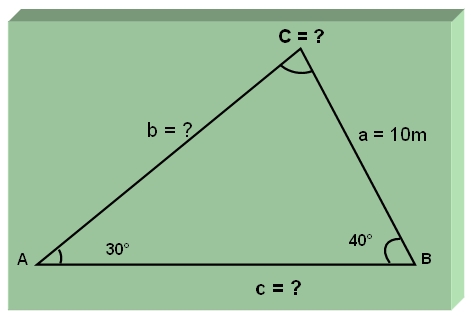
Enlaces externos para explorar
- Conceptos de Física: Hyperphysics
- Libros:
- Simulaciones: PhET
- Tutorial de Física en Inglés: Physics Classroom
- Wikipedia en Español: Wikipedia
Presentación
Vídeo
Ley del seno
Páginas recientes
- Carl Friedrich Gauss: Matemática y Física
- La IA Revoluciona la Investigación
- Ernest Rutherford y su Legado
- Antoine Henri Becquerel y la Radiactividad
- La Ocultación en Astronomía
- Escribiendo el Póster de la Investigación
- Presentando la Investigación – Poster
- Movimiento de Traslación en el Universo
- Movimiento de Rotación en el Universo
- Webquest: Explorando el Universo
- Metodo, Procedimiento e Investigación
- Maria Skłodowska-Curie y la Radiactividad
- Investigando el Desplazamiento de Wien
- El Hielo, la Nieve y la Lluvia Helada
- Niels Bohr y la Estructura Atómica
Más páginas para explorar
-

¡Vistiendo para el Espacio!
-

Abstract: Resumen Breve de Investigación
-

Aceleración en Caída Libre
-

Aceleración Grativacional en Planetas
-

Aceleración Gravitacional en la Tierra
-

Aceleración Lineal y sus Representaciones
-

Aisladores y Conductores
-

Alacena virtual de conversiones
-
Albert Einstein Historia y Vida
-
Alessandro Volta y la Electricidad
-

Amedeo Avogadro y su Ley
-
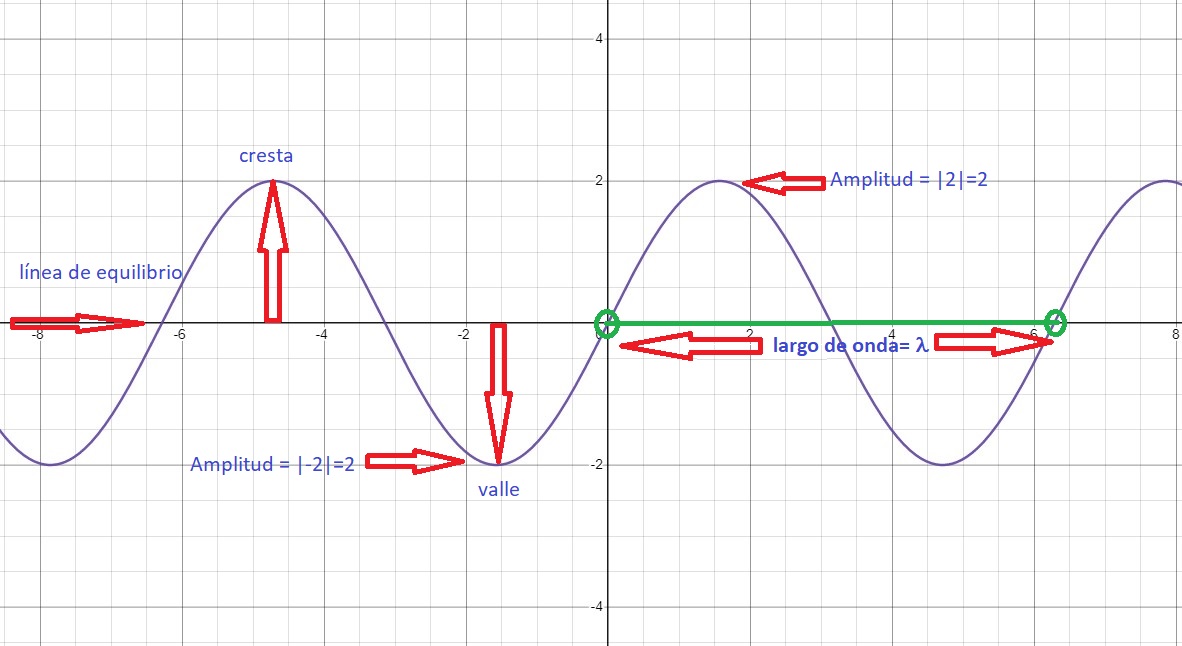
Amplitud, largo de onda y frecuencia
-

Análisis Gráfico del Movimiento
-

Andrés Ampere y el Electromagnetismo
-

Antoine Henri Becquerel y la Radiactividad
-

Ernest Rutherford y su Legado
-

Antoine Henri Becquerel y la Radiactividad
-
La Ocultación en Astronomía
-
Trigonometría: Un Mundo de Ángulos

La trigonometría es una rama de las matemáticas que se dedica al estudio de las relaciones entre los lados y los ángulos de los triángulos.
-
Temperatura: Una Medida de Energía

La temperatura es una propiedad física e intensiva de la materia que no depende de la cantidad de materia ni promueve el cambio estructural de la misma.
-
Sistema Internacional Unidades y Ciencia

El Sistema Internacional de Unidades, comúnmente abreviado como SI, es un sistema de medidas que se utiliza como referencia en casi todos los países del mundo.













