
Objetivos:
Al terminar esta la lección:
- Definirás las funciones trigonométricas a partir de la geometría del triángulo rectángulo.
- Explicarás como medir los ángulos de un triángulo.
- Utilizarás las funciones trigonométricas para hallar las medidas desconocidas de un triángulo rectángulo.
- Seleccionarás correctamente la función trigonométrica apropiada para resolver los problemas.
La Trigonometría
La trigonometría es una rama de las matemáticas que se dedica al estudio de las relaciones entre los lados y los ángulos de los triángulos. 1 En esencia, nos permite analizar y calcular medidas de triángulos, lo cual es fundamental en muchas áreas de la ciencia y la ingeniería.
Los ángulos
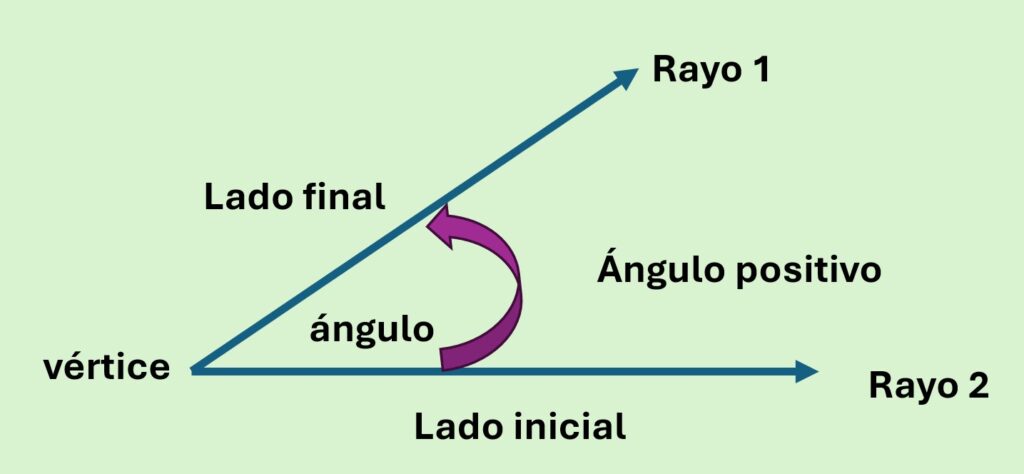
Un ángulo se define como el resultado de la intersección de dos rayos. Los rayos que componen el ángulo se denominan lados, mientras que el unto de intersección se denomina vértice.
Trigonometría
En la trigonometría suele distinguirse entre los lados del ángulo, llamándolos lado inicial y lado final. Es muy común en pensar en los ángulos como el resultado de la rotación de uno de los rayos desde el lado inicial hasta el lado final con el vértice fijo.
Si la rotación ocurre en contra de las manecillas del reloj, se dice que el ángulo es positivo; si por el contrario el rayo rota en dirección de las manecillas del reloj, decimos que el ángulo es negativo.
Unidades
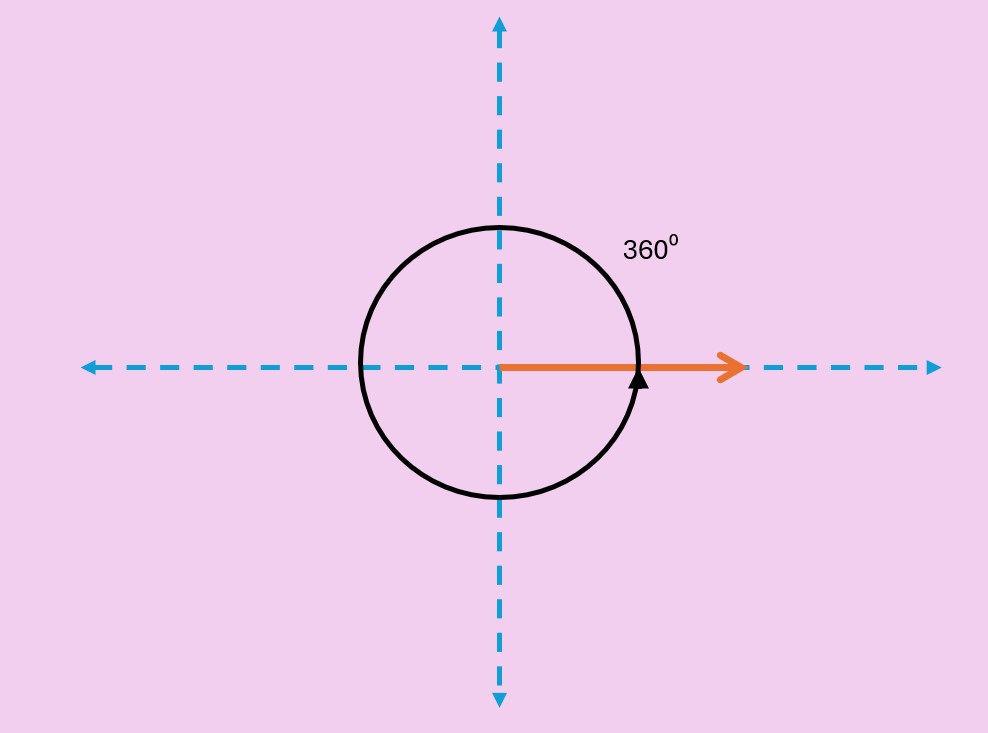
Existen varias unidades para medir los ángulos, las más comunes son los grados y los radianes. En esta lección utilizaremos los grados como la unidad para expresar la medida de los ángulos. Se define un grado como 1/360 de la rotación completa del rayo.
Ángulos Positivos y Negativos
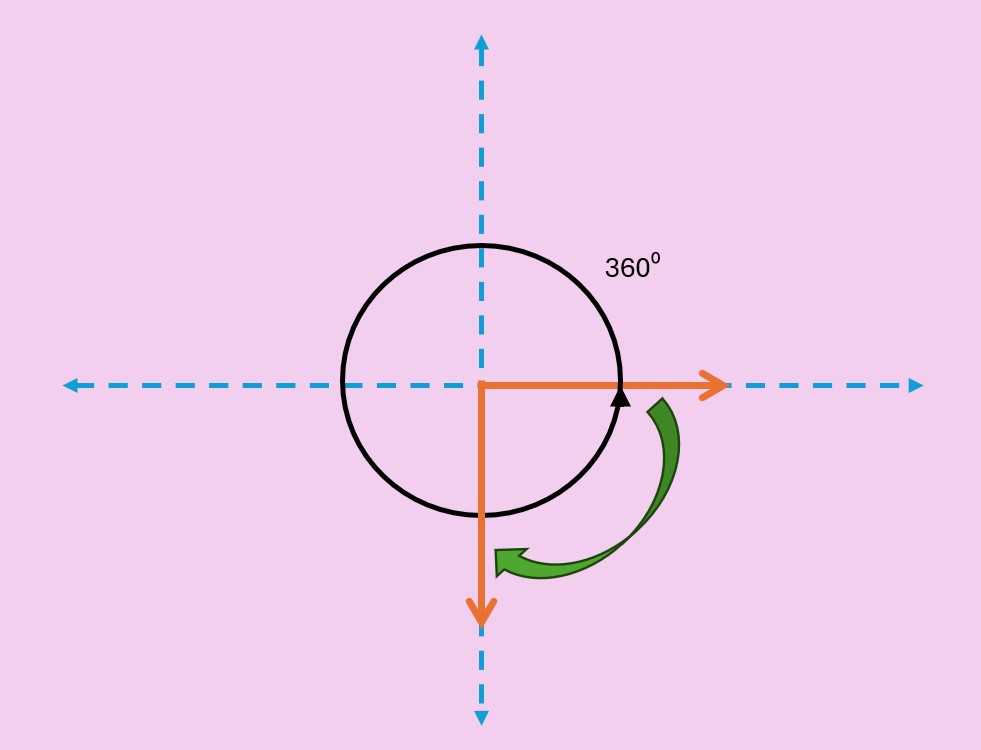
La medida del ángulo puede ser positiva o negativa. Depende de la dirección en que rotara el rayo que forma el ángulo. Por ejemplo, el ángulo formado por una rotación completa en contra de las manecillas del reloj, tiene una medida de 360°.
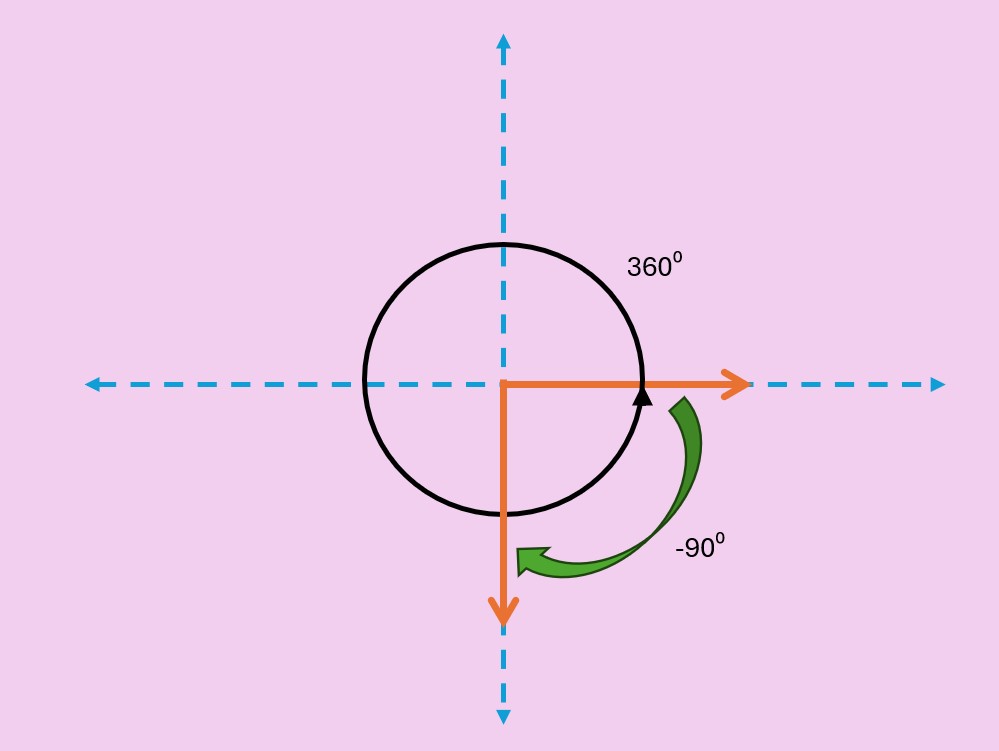
Un cuarto de rotación a favor de las manecillas del reloj, forma un ángulo cuya medida es de -90°.
El ángulo de cero grados
Un ángulo de 0° resulta cuando no ocurre la rotación y ángulos mayores de 360° son posibles si pensamos en una rotación más allá de una revolución completa.
Por ejemplo, dos rotaciones completas a favor de las manecillas del reloj producen un ángulo de -720°, mientras que tres rotaciones producirían un ángulo de 1080°.
Ahora que ya sabes medir ángulos podemos hablar de los triángulos rectángulos.
Los triángulos rectángulos
Los triángulos son figuras geométricas con tres lados y tres ángulos. Existen varios tipos de triángulos, entre ellos el triángulo rectángulo. Este tipo de triángulo se caracteriza por tener uno de sus ángulos con medida igual a 90°. A este ángulo también se le conoce como ángulo recto. La suma de todos los ángulos en un triángulo es de 180°. En el caso de los triángulos rectángulos, como el ángulo recto mide 90°, entonces los otros dos ángulos sumados son igual a 90°.
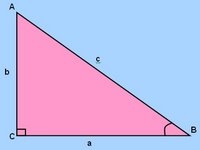
La Hipotenusa
El lado que queda opuesto o de frente al ángulo recto, siempre es el lado más largo. A este lado lo denominamos hipotenusa. Los otros dos lados del triángulo lo denominamos catetos. Así que los lados de un triángulo rectángulo están compuestos por la hipotenusa y los catetos. Al igual que con los ángulos de los triángulos, existe una relación entre los catetos y la hipotenusa. Según postulara el matemático Pitágoras en su teorema, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Esto está dado por la siguiente ecuación:
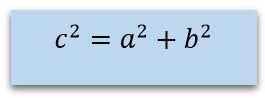
Funciones trigonométricas
La trigonometría es el estudio de la relación entre los lados y los ángulos del triángulo rectángulo. Muchas aplicaciones de la trigonometría dependen de esta relación. A estas relaciones las denominamos funciones trigonométricas.
Triángulo con Vértice C
Sea el triángulo ACB un triángulo rectángulo con el ángulo recto en el vértice C. Sus lados a y b son sus catetos y el lado c la hipotenusa. Cada ángulo, en el triángulo tiene un lado opuesto, lado de frente al ángulo, y un lado adyacente, lado que forma parte del ángulo en cuestión.
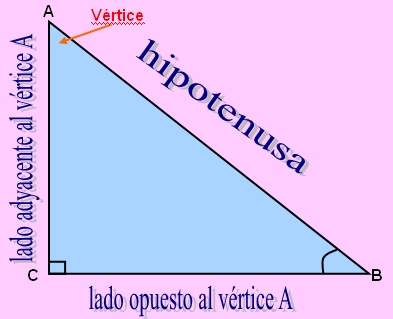
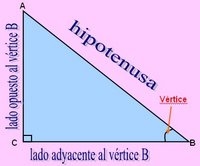
El vértice
De la forma en que ha sido configurado el triángulo en este ejemplo, el vértice A tiene al cateto a como lado opuesto y al cateto b como lado adyacente. De igual forma el vértice B tiene al cateto b como lado opuesto y al cateto a como lado adyacente. Los lados opuestos y adyacentes se intercambian entre sí para los dos ángulos que no son el ángulo recto en el triángulo rectángulo.
En el caso del ángulo recto, hay que notar que tiene como lado opuesto a la hipotenusa y no tiene lado adyacente. El identificar los lados opuestos y adyacentes respecto a un ángulo es sumamente importante a la hora de definir las funciones trigonométricas.
En esta unidad solamente definiremos las tres funciones trigonométricas básicas: seno, coseno y tangente. Estas son:
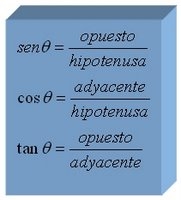
Existen otras funciones trigonométicas como sec θ, csc θ y cot θ. Estas se pueden definir en términos de las funciones principales de sen θ, cos θ y tan θ. Por esta razón en Física se trata de usar las cantidades fundamentales y es más conveniente utilizarlas para resolver problemas.
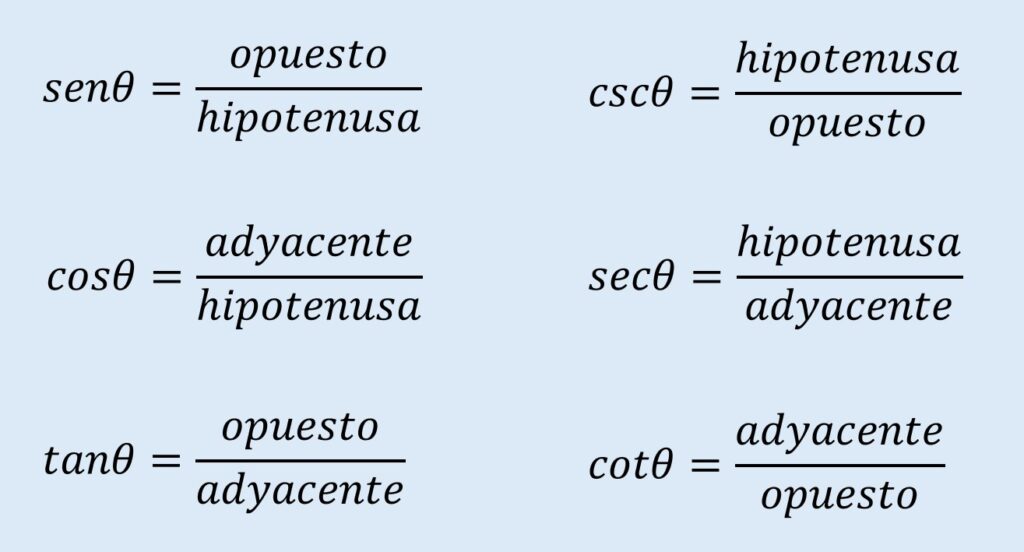
Ejemplo 1: Altura del faro
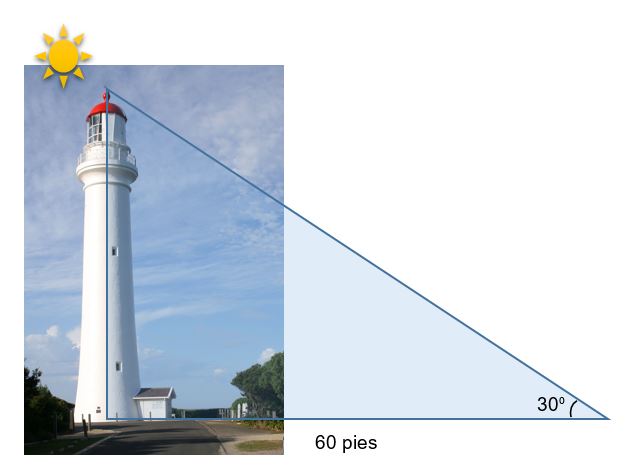
Imagina que deseas saber la altura de un faro y lo único que conoces es que la sombra del mismo mide unos 60 pies de longitud desde la base del faro. También conoces que el Sol se encuentra en un ángulo ascendente de 30º.
¿Cómo determinar la altura del faro?
Esta y otras preguntas las podemos contestar con un conocimiento básico de trigonometría. En esta lección estudiaremos las funciones trigonométricas en términos de los ángulos y su aplicación en el estudio de los triángulos rectángulos. Los datos que nos brinda este ejemplo son los siguientes:
- distancia de la base, a = 60 pies
- ángulo del sol, θ= 30°
- desconocida altura, b=?

El resultado para este ejemplo es aproximadamente 34.6 pies.
La función de seno de un triángulo
La función seno (sen θ) de un ángulo, se define como la proporción que existe entre el lado opuesto y la hipotenusa. Esta función aplica para un triángulo rectángulo y se utiliza como parte fundamental de la trigonometría básica. Matemáticamente esta proporción se expresa como:
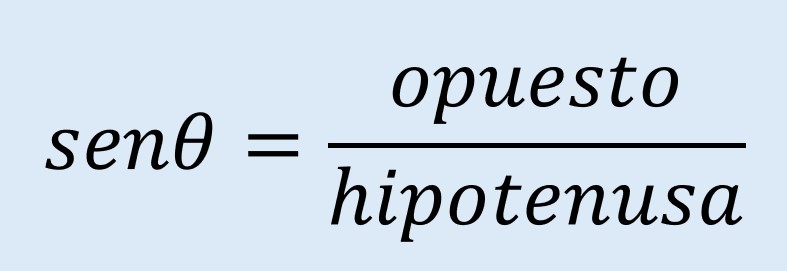
Donde el símbolo θ se utiliza para denotar el ángulo que estaremos considarando.
Ejemplo 2: Resuelve el triángulo
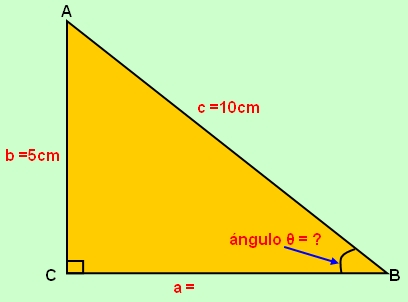
Observa la figura. La figura presenta un triángulo rectángulo. Este triángulo presenta unas cantidades marcadas en los lados correspondientes. Si su lado opuesto mide 5.0 cm y la hipotenusa es igual a 10.0 cm. Entonces podemos calcular el ángulo θ.
Entonces tenemos un problema que podemos resolver. Primero debemos identificar los datos:
- lado opuesto, b = 5.0 cm
- hipotenusa, c=10.0 cm
- desconocido el ángulo, θ=?
El procedimiento para resolverlo es el siguiente:

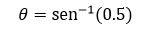
Observa que los valores de las funciones trigonométricas no tienen unidades ya que se cancelan. Ahora debemos identificar cuál es el ángulo θ cuya relación entre sus lados es 0.5.
Esta función se lee seno inverso del ángulo theta. Por lo tanto el ángulo que tiene una relación de sen de θ igual a 0.5 o ½, correspondiente es igual a 30°.
Coseno
La función coseno (cos θ) se define como la proporción entre el lado adyacente y la hipotenusa. Esta función se expresa con sus lados adyacente e hipotenusa segúm muestra la figura.
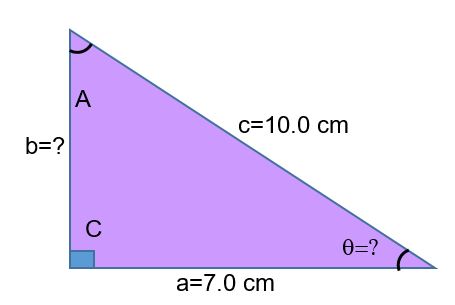
Ejemplo 3: Coseno inverso
Sea el ángulo igual a 45° y su lado adyacente igual a 7.0 cm y la hipotenusa igual a 10.0 cm. Los datos son los siguientes:
- lado adyacente, a = 7.0 cm
- hipotenusa, c = 10.0 cm
- ángulo desconocido, θ=?
Para resolver el problema es necesario hacer lo siguiente:

Puedes notar que se utilizó la función de coseno inverso para obtener el ángulo.
Esta función se lee “coseno inverso” pero su significado es el el recíproco de la función lo cual representa un número que nos da el ángulo correspondiente. Puedes usar la calculadora para obtener el resultado. La respuesta para el ángulo θ es el ángulo de 45°.El triángulo básico que mejor nos muestra esta relación es:
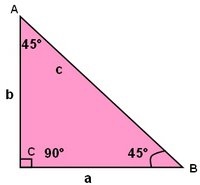
Tangente
La función tangente se define como la proporción entre el lado opuesto y el adyacente. Esta función se expresa según lo muestra la siguient figura.
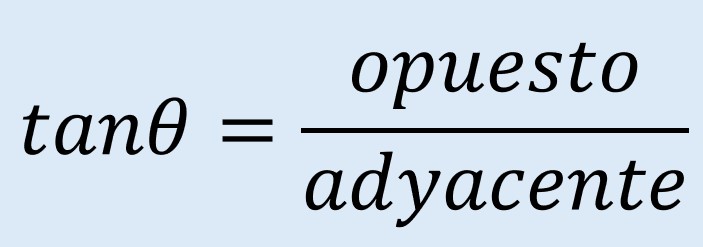
Ejemplo 4: Tangente inversa
Si el lado opuesto de un triángulo es igual a 8.00 cm y el lado adyacente igual a 4.62 cm, determina el ángulo θ desconocido.
Los datos son los siguientes:
- lado opuesto, b = 8.00 cm
- lado adyacente, a = 4.62 cm
- ángulo desconocido, θ = ?
Para resolverlo es necesario el siguiente procedimiento:

Entonces la tangente inversa de 1.73 es 60°. Para revisar los cálculos provistos puedes usar una calculadora. Es importante que sepas como realizar el procedimiento. Para revisar los cálculos aquí demostrados y sustituir otras cantidades en los ejemplos demostrados utiliza la calculadora.
El mejor triángulo que representa la situación del ejemplo es: el de 60 grados.
Presentación
Simulación
Vector Addition
Enlaces externos para explorar
- Conceptos de Física: Hyperphysics
- Libros:
- NASA: Science Explorer Poster Series
- Simulaciones: PhET
- Tutorial de Física en Inglés: Physics Classroom
- Wikipedia en Español: Wikipedia
Vídeo
Funciones trigonométricas
Teorema de Pitágoras
Páginas recientes
- La Ocultación en Astronomía
- Escribiendo el Póster de la Investigación
- Presentando la Investigación – Poster
- Movimiento de Traslación en el Universo
- Movimiento de Rotación en el Universo
- Webquest: Explorando el Universo
- Metodo, Procedimiento e Investigación
- Maria Skłodowska-Curie y la Radiactividad
- Investigando el Desplazamiento de Wien
- El Hielo, la Nieve y la Lluvia Helada
- Niels Bohr y la Estructura Atómica
- Stephen Hawkings: Pionero de Física
- Alessandro Volta y la Electricidad
- Momento Angular: Relación con el Torque
- Carl Sagan: Un Visionario
-
Compara Balanzas: Análoga o Digital
La balanza es una palanca de primer grado que tiene dos brazos de igual tamaño, Mediante el equilibrio entre los pesos de dos cuerpos comparas sus masas.
-
Herramientas Para Medir la Masa

La balanza es una palanca de primer grado que tiene dos brazos de igual tamaño, Mediante el equilibrio entre los pesos de dos cuerpos comparas sus masas.
-
Trigonometría: Un Mundo de Ángulos

La trigonometría es una rama de las matemáticas que se dedica al estudio de las relaciones entre los lados y los ángulos de los triángulos.












