Parte 7: Problemas de velocidad vs tiempo – Soluciones

Objetivos
Terminada la lección podrás:
- Resolver problemas de velocidad versus tiempo.
Parte 7: Problemas de velocidad versus tiempo – Soluciones
Solución para el Problema de Práctica 1
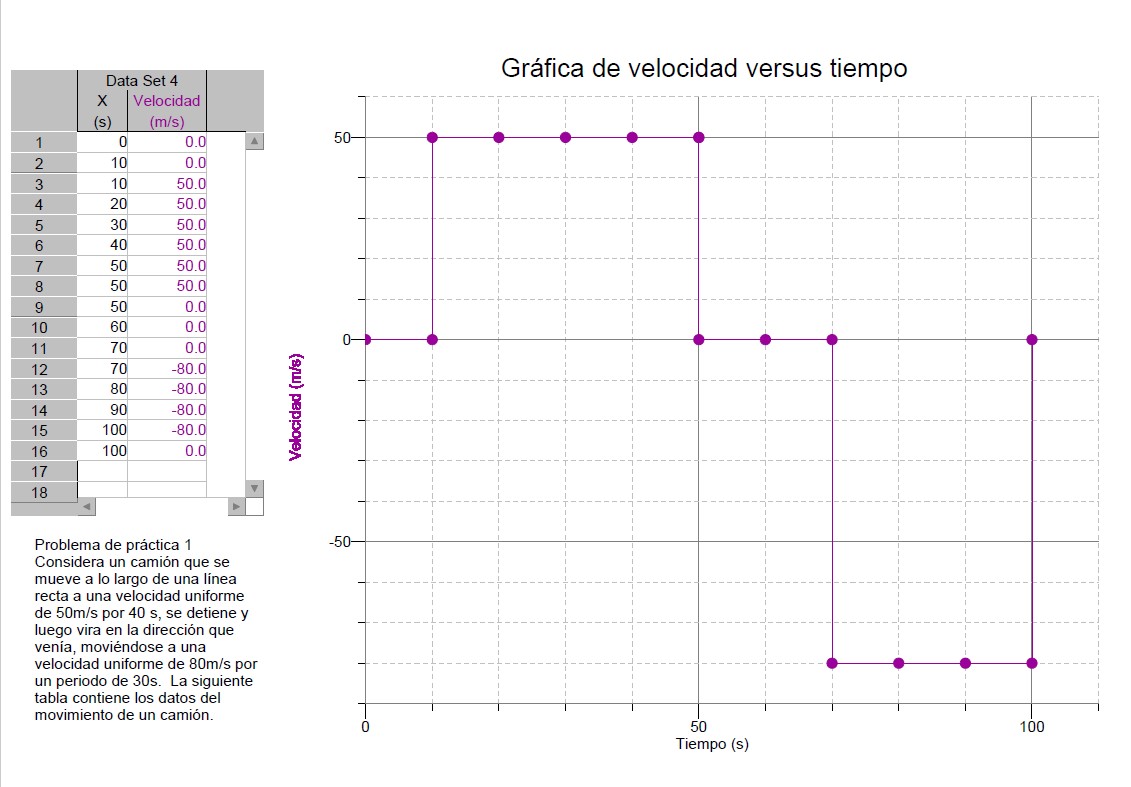
1. La siguiente tabla contiene los datos del movimiento de un camión. Haz un diagrama para demostrar el movimiento del camión y dibuja la gráfica.
| Punto | Tiempo (s) | Velocidad (m/s) |
| A | 0 | 0 |
| B | 10 | 0 |
| C | 10 | 50 |
| 20 | 50 | |
| 30 | 50 | |
| 40 | 50 | |
| D | 50 | 50 |
| E | 50 | 0 |
| 60 | 0 | |
| F | 70 | 0 |
| G | 70 | -80 |
| 80 | -80 | |
| 90 | -80 | |
| H | 100 | -80 |
| I | 100 | 0 |
La gráfica original que utilizaste para contestar el ejercicio de práctica la puedes visualizar aquí abajo. Las gráficas que mejor demuestran la relación entre las cantidades son las siguientes:
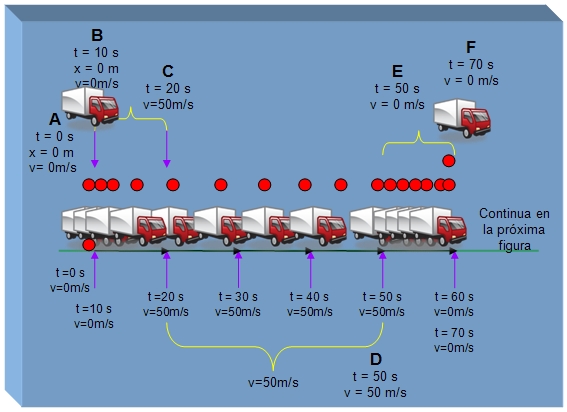
Para que puedas entender mejor lo que ocurre estamos representando todo con dibujos y una escala de tiempo que aparece en la parte de abajo de los camiones. También representamos las posiciones con letras para que puedas entender físicamente lo que ocurre en cada punto.
Camión detenido
Observa en la imagen que el camión se queda detenido durante los primeros 10 segundos, justo en 20 segundos e instantáneamente cambia su velocidad a 50m/s durante 30 segundos, es decir, continua a una velocidad de 50m/s hasta 50 segundos donde frena o reduce la velocidad instantáneamente hasta detenerse según se aprecia en el punto E. Sigue detenido durante 20 segundos hasta llegar a los 70 segundos que cubre la figura anterior. Ahora mira lo que sucede en la próxima imagen.
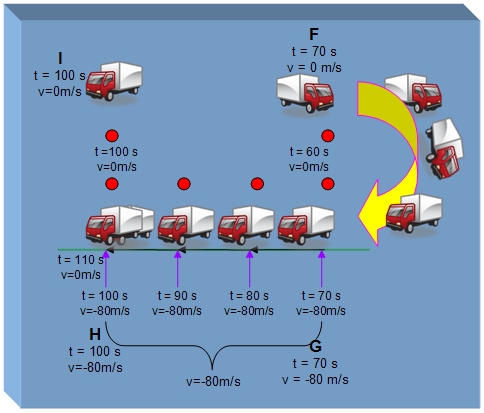
El camión que estaba detenido, inmediatamente cambia de dirección por eso la velocidad tiene un signo negativo, como puedes observar en la figura.
Aumento en la velocidad
El camión aumenta su velocidad de forma instantánea a 80m/s y sigue moviéndose hasta alcanzar los 100 segundos de la trayectoria. Puede que tu gráfica no sea igual a esta representación y si muy parecida a la siguiente:
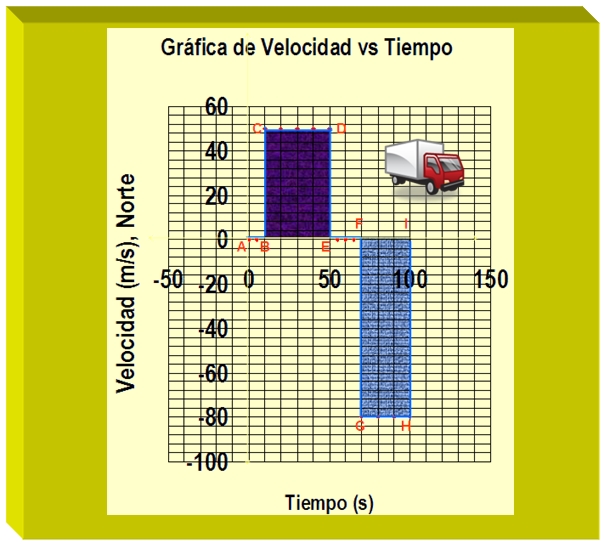
Esta gráfica es la mejor representación del evento que está indicado en los datos de la tabla.
Llena la tabla
2. Determina la forma de la gráfica, la velocidad, el desplazamiento y el desplazamiento total según puedas determinarlo en cada tramo. Para esto llena la tabla de datos que aparece a continuación.
Esta es la respuesta a la tabla de la gráfica
| Tramo | Forma: | Velocidad (m/s) | Tiempo (s) | Desplazamiento (m) | Desplazamiento Total (m) |
| AB | Lineal Horizontal | No tiene | Aumenta de 0 a 10s Δt = 10 s | No hay desplazamiento | No hay desplazamiento |
| BC | Lineal vertical | Aumenta instantáneamente de 0m/s a 50 m/s, Norte ΔV = 50 m/s | Constante en 10s Δt = 0 s | No hay datos suficientes | No hay datos suficientes |
| CD | Lineal Horizontal | Constante en 50m/s, N ΔV = 0 m/s | Aumenta de 10s a 50 s Δt = 40 s | 50m/s X 40s 2,000 m, N | 2,000 m, N |
| DE | Lineal vertical | Disminuye instantáneamente de 50m/s a 0 m/s, Norte ΔV = 50 m/s | Constante en 50s Δt = 0 s | No hay datos suficientes | 2,000m, N |
| EF | Lineal Horizontal | No hay velocidad, no hay movimiento ΔV=0m/s | Aumenta de 50s a 70s Δt = 20 s | No hay movimiento d=0m | 2000m, N |
| FG | Lineal vertical | Aumenta instantáneamente de 0m/s a 80 m/s, Sur ΔV = 80 m/s | Constante en 70s Δt = 0 s | No hay datos suficientes | 2000m, N |
| GH | Lineal Horizontal | Constante en 80m/s, S ΔV = 0 m/s | Aumenta de 70s a 100 s Δt = 30 s | 80m/s X 30s 2,400 m, S | +2,000m +(-2,400m) = -400m =400m, S |
| HI | Lineal vertical | Aumenta instantáneamente de 0m/s a 80 m/s, Sur ΔV= 80 m/s | Constante en 70s Δt = 0 s | No hay datos suficientes | 400m,S |
Comentarios para la tabla de datos
En el tramo de AB no hay desplazamiento porque no hay movimiento.
El tramo de BC tiene una velocidad que aumenta instantáneamente por lo que este cambio tan abrupto no nos permite calcular el desplazamiento con los datos que tenemos.
Velocidad constante
En el tramo de CD la velocidad se mantiene constante. A medida que el tiempo transcurre el camión se va desplazando. Su desplazamiento se puede calcular así:
d = v x t = (50 m/s)(40 s) = 2,000 m
d = 2,000 m , Norte
- En el tramo de DE la velocidad disminuye instantáneamente en dirección Norte. El cambio en la velocidad es de 50m/s.
- En el tramo EF la rapidez es cero, se mantiene en la misma posición, por lo tanto no hay desplazamiento, aunque han transcurrido 20 segundos.
- En el tramo de FG la forma de la gráfica es lineal vertical. Hay un aumento instantáneo de la velocidad pero en dirección Sur.
- Esto significa que el camión se mueve en dirección opuesta a la que se movía inicialmente. Es por esta razón que la velocidad tiene el signo negativo.
- No podemos determinar cuanto es el desplazamiento porque no tenemos suficientes datos para calcularlo.
Desplazamiento
En el tramo de GH podemos calcular el desplazamiento de la siguiente forma:
d = v x t = (80 m/s)(30 s) = 2,400 m
d = 2,400 m, Sur
Al final el camión regresó a la posición original y se desplazó más allá de la misma por 400m. Para calcular el desplazamiento total tenemos que considerar el desplazamiento de 2,000 m, Norte al cual le pondremos signo positivo y los 2,400m en dirección Sur al cual le pondremos signo negativo. El procedimiento sería el siguiente:
dtotal = +2,000m – 2,400m = – 400m = 400m, Sur
La distancia total recorrida es la suma de la magnitud de los desplazamientos: dtotal = 4,400 m
Solución del problema 2
Esta es la gráfica:
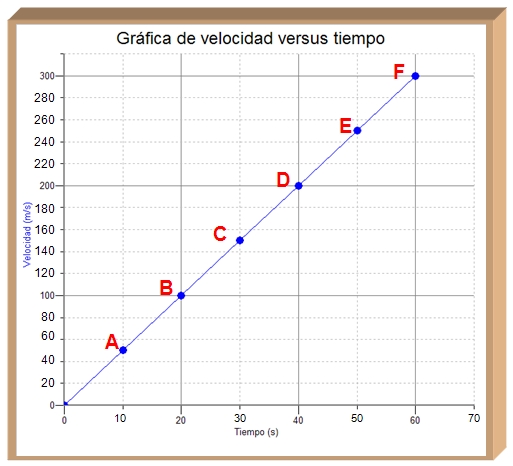
Puedes ver la gráfica abajo:
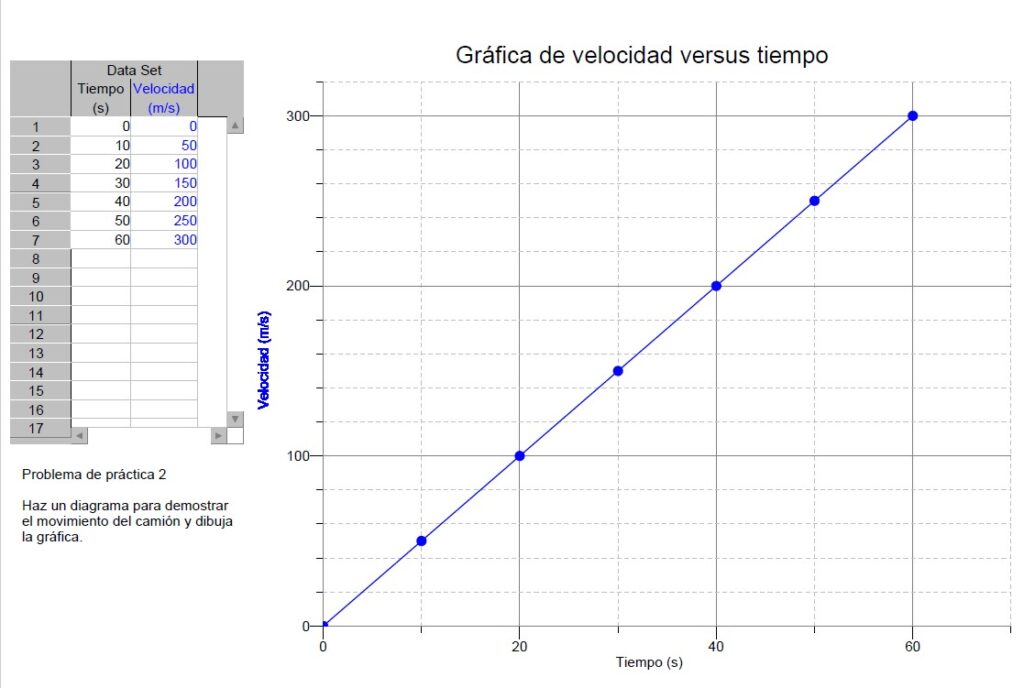
Esta es la respuesta para la tabla:
| Tramo | Forma: | Velocidad (m/s) | Tiempo (s) | Aceleración (m/s2) | Desplazamiento (m) | Desplazamiento Total (m) |
| AB | Lineal Ascendente | Aumenta de 0 a 100m/s, N ΔV = 100 m/s | Aumenta de 0 a 20s Δt = 20 s | ΔV /Δt = 100m/s/20s =5m/s2 | A= ½ bh= ½ (20s)(100m/s) = 1,000 m, Norte | 1,000m, Norte |
| BC | Lineal Ascendente | Aumenta de 100 a 200m/s, N ΔV = 100 m/s | Aumenta de 20 a 40s Δt = 20 s | ΔV /Δt = 100m/s/20s =5m/s2 | A= ½ bh + L X a = =½ (20 s)(100m/s) + (100m/s)(20s) =1000m+2000= 3,000m, Norte | 1000m + 3000m =4,000m, Norte |
| CD | Lineal Ascendente | Aumenta de 200 a 300m/s, N ΔV = 100 m/s | Aumenta de 40 a 60s Δt = 20 s | ΔV /Δt = 100m/s/20s =5m/s2 | A= ½ bh + L X a = ½ (20 s)(100m/s) + (200m/s)(20 s) =1000m+4000m= =5,000m, Norte | = 4,000m +5,000m =9,000 m, Norte |
Esta es la respuesta de la segunda tabla que recoge los datos de la toda la gráfica:
| Tramo | Forma: | Velocidad (m/s) | Tiempo (s) | Aceleración (m/s2) | Desplazamiento (m) | Desplazamiento Total (m) |
| AD | Lineal Ascendente | Aumenta de 0 a 300m/s, N ΔV = 300 m/s | Aumenta de 0 a 60s Δt = 60 s | ΔV /Δt = 300m/s/60s =5m/s2 | A= ½ bh = ½ (60 s)(300m/s)= 9,000m, Norte | 1,000m + 3,000m +5,000m = =9,000 m, Norte |
Observa el desplazamiento en ambas tablas, ¡son iguales! No importa el procedimiento que uses debes seguir las reglas del álgebra y la aritmética para obtener el mismo resultado demostrado en ambas tablas.
Solución problema de práctica 3
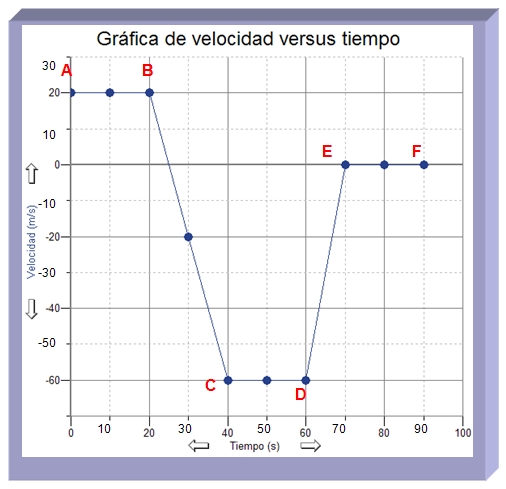
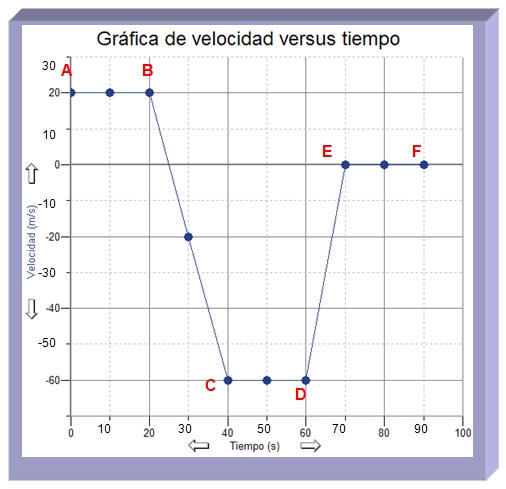
La siguiente tabla tiene los datos de un auto que se mueve en una autopista.
| Tiempo (s) | Velocidad (m/s) |
| 0 | 20 |
| 10 | 20 |
| 20 | 20 |
| 30 | -20 |
| 40 | -60 |
| 50 | -60 |
| 60 | -60 |
| 70 | 0 |
| 80 | 0 |
| 90 | 0 |
Instrucciones:
- Describe todos los intervalos que se presentan en la gráfica de la izquierda en términos de la forma, velocidad, tiempo, aceleración, distancia y desplazamiento. Utiliza la siguiente tabla para recopilar los resultados:
- Explica el movimiento del mismo en términos de su posición, distancia, desplazamiento, rapidez y velocidad. Indica en cuales momentos de la gráfica no hay movimiento.
- En el único tramo que no hay movimiento en el tramo EF debido a que la velocidad es 0m/s.
Puedes bajar la gráfica en el siguiente enlace:
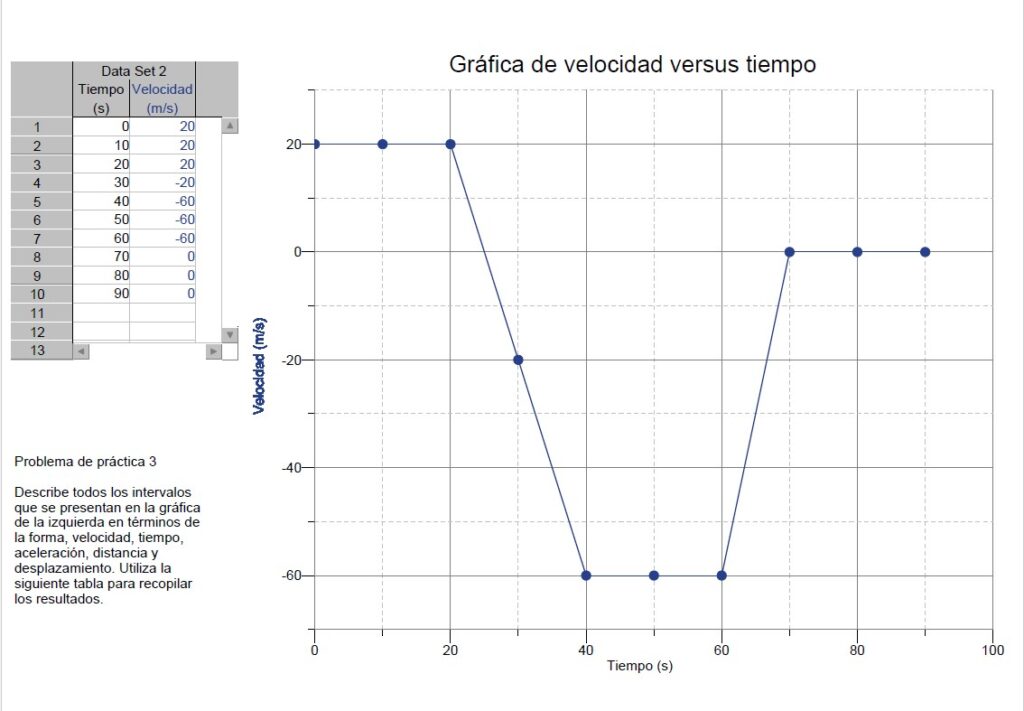
Llena la siguiente tabla:
| Tramo | Forma: | Velocidad (m/s) | Tiempo (s) | Aceleración (m/s2) | Desplazamiento (m) | Desplazamiento Total (m) |
| AB | Lineal Horizontal | Constante en 20 m/s, Norte ΔV = 0 m/s | Aumenta de 0 a 20s Δt = 20 s | 0m/s2, no hay | A= L X a = (20m/s) (20s) = 400m 400m, Norte | 400m, Norte |
| BC | Lineal Descendente | Disminuye de 20m/s a 0, Norte se detiene en 30s. Cambia de dirección y aumenta la velocidad de 0 a 60 m/s, SurΔV = 80 m/s | Aumenta de 20 a 40s Δt = 20 s | a=ΔV /Δt =80m/s/20s =4 m/s2 los primeros 5 segundosy luego acelera con esa magnitud | A= ½ bh = ½ (5s) (10m/s) = =25m, Norte A= ½ bh = ½ (15s) (60m/s) = =450m, Sur Para calcular el desplazamiento restas: 25m – 450m Dtotal=(-425 m)= 425m, Sur distancia = (25m)+(450m) = =500m | +400m+(-425m)= =(-25m) Dtotal=25m, Sur |
| CD | Lineal Horizontal | Constante en 60 m/s, Sur ΔV = 0 m/s | Aumenta de 40 a 60s Δt = 20 s | 0m/s2, no hay | A= L X a = (20s) (30m/s) = =600m, Sur | =(-600m)+(-25m) =(-625 m) =625 m, Sur |
| DE | Lineal Ascendente | Disminuye de 60m/s a 0, Sur. Se mueve hacia el sur ΔV = -60 m/s | Aumenta de 60 a 70s Δt = 10 s | a=ΔV /Δt = =-60m/s/10s =-6m/s2 decelera o frena | A= ½ bh =½ (10s)(60m/s)= =300m, Sur | (-625m)+(-300m) =(-925m) =925m, Sur |
| EF | Lineal Horizontal | No hay, no se mueve, constante en 0m/s ΔV = 0 m/s | Aumenta de 70 a 90s Δt = 20 s | 0m/s2, no hay | A= L X a =0m No hay movimiento por lo tanto no hay desplazamiento | El desplazamiento total es de 925m, Sur |
En este ejercicio debiste notar que el objeto comienza a moverse hacia el norte y luego cambia de dirección moviéndose hacia el sur durante la mayor parte de su recorrido, desde t=a 25 s hasta t=70s.
Regresar a la página de Gráficas de velocidad versus tiempo 2
Problema de práctica 4
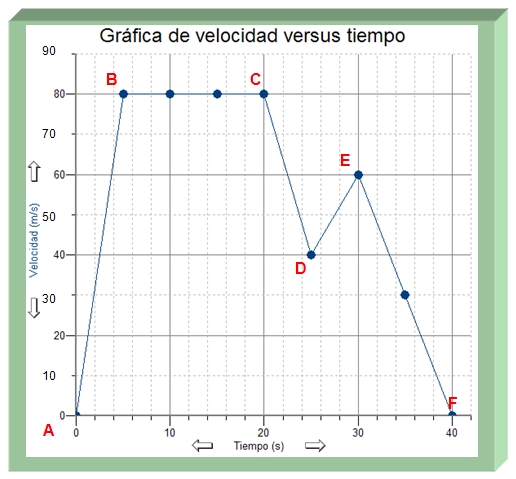
Instrucciones:
La siguiente gráfica muestra el movimiento de un tren. Describe todos los intervalos que se presentan en la gráfica de la derecha en términos de la forma, velocidad, tiempo, aceleración, distancia y desplazamiento.
Puedes bajar la gráfica en el siguiente enlace:
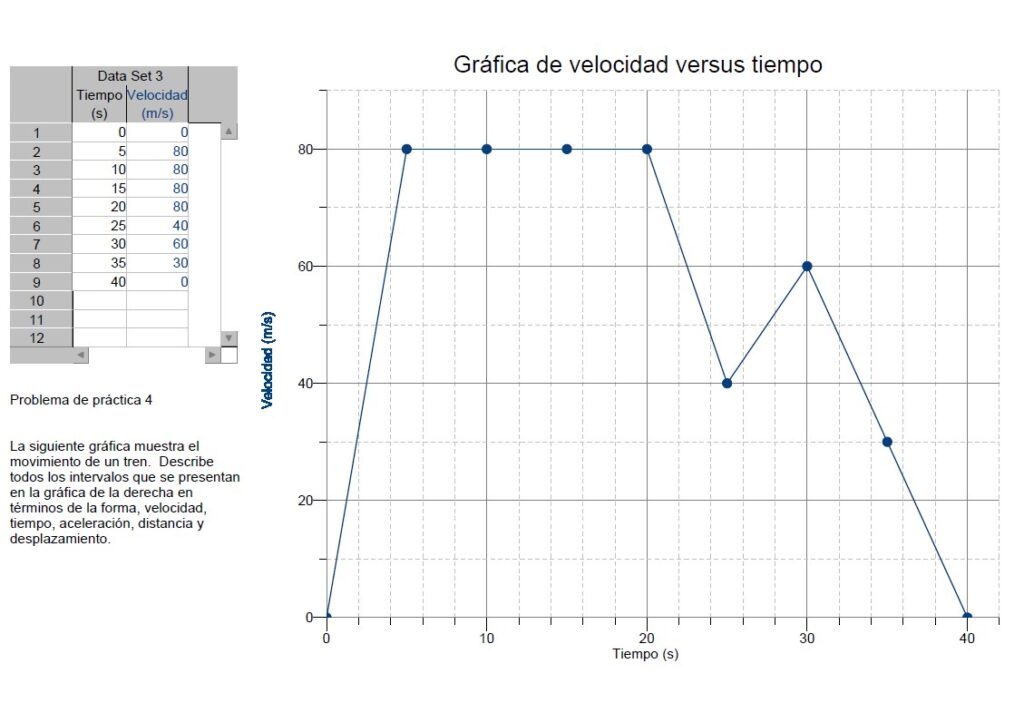
Gráfica de velocidad vs tiempo para contestar el problema de práctica 4
Tabla de datos – Respuesta
Utiliza la siguiente tabla para recopilar los resultados:
| Tiempo (s) | Velocidad (m/s) |
| 0 | 0 |
| 5 | 80 |
| 10 | 80 |
| 15 | 80 |
| 20 | 80 |
| 25 | 40 |
| 30 | 60 |
| 35 | 30 |
| 40 | 0 |
Indica en cuales momentos disminuyó la velocidad. ¿Cambió de dirección en algún momento?
La velocidad disminuyó en los tramos CD y en EF. El tren se mantiene moviéndose en la misma dirección.
Tabla de datos – Respuesta
Llena la siguiente tabla con las respuestas correspondientes. Explica en tus palabras lo que ocurre en cada tramo de la gráfica.
| Tramo | Forma: | Velocidad (m/s) | Tiempo (s) | Aceleración (m/s2) | Desplazamiento (m) | Desplazamiento Total (m) |
| AB | Lineal Ascendente | Aumenta de o a 80m/s, Norte ΔV = 80 m/s. | Aumenta de 0 a 5s Δt = 5 s | a=ΔV /Δt =80m/s/5s =16m/s2,Norte acelera | A= ½ bh = ½ (5s) (80m/s) = desplazamiento= 200m, Norte distancia = 200m | =200m, Norte |
| BC | Lineal Horizontal | Constante en 80 m/s, Norte ΔV = 0 m/s. | Aumenta de 5 a 20 s Δt = 15 s | 0m/s2, no hay | A= L X a = (80m/s) (150s) = desplazamiento= 1200m, Norte distancia= 1200m | =+200m+(1200m) =+1400m Dtotal=1400m, Norte |
| CD | Lineal Descendente | Disminuye de 80m/s a 40m/s, Norte ΔV = -40 m/s | Aumenta de 20 a 25s Δt = 5 s | a=ΔV /Δt =-40m/s/5s = -8m/s2, Norte frena o decelera | A= ½ bh = ½ (5s) (40m/s) = =100m, Norte A= L X a = (5s) (40m/s) =200m, Norte Para calcular el desplazamiento sumas: 100m + 200m Dtotal=(300 m)= 300m, Norte distancia = 300m | =(1400m)+(300m) =(+1700 m) =1700 m, Norte |
| DE | Lineal Ascendente | Aumenta de 40m/s a 60m/s, Norte ΔV = 20 m/s | Aumenta de 25 a 30s Δt = 5 s | a=ΔV /Δt = =20m/s/5s = 4m/s2 acelera | A= ½ bh = ½ (5s) (20m/s) = =50m, Norte A= L X a = (5s) (40m/s) = =200m, Norte Para calcular el desplazamiento sumas: 50m + 200m = Dtotal=(250 m)= 250m, Norte distancia = 250m | =(1700m)+(250m) =(+1950m) =1950m, Norte |
| EF | Lineal Descendente | Disminuye de 60 m/s a 0m/s, Norte ΔV = -60 m/s | Aumenta de 30 a 40s Δt = 10 s | a=ΔV /Δt =-60m/s/10s = -6m/s2, Norte frena o decelera | A= ½ bh =½ (10s)(60m/s)= desplazamiento=300m, Norte distancia= 300m | =1950m+300m =+2250m El desplazamiento total es de 2250m, Norte |
Regresar a la página de Gráficas de velocidad versus tiempo 2
Problema de práctica 5 – Solución
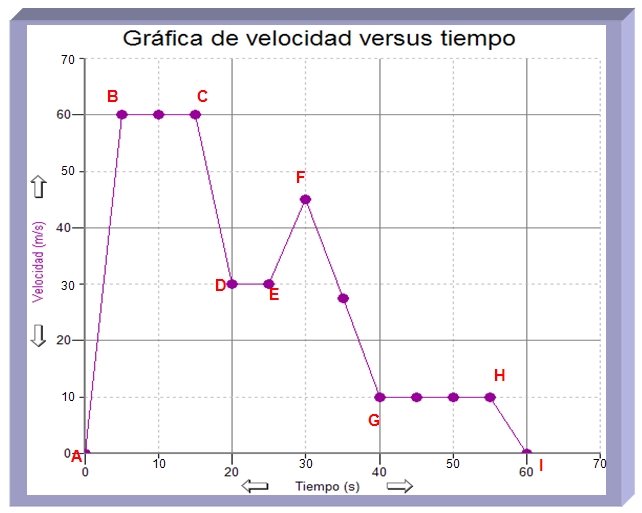
Un camión se mueve a lo largo de una autopista como lo presenta la siguiente gráfica. Sigue las instrucciones y explica la gráfica correctamente.
Instrucciones:
Describe todos los intervalos que se presentan en la gráfica de la derecha en términos de la forma, velocidad, tiempo, aceleración, distancia y desplazamiento. Utiliza la siguiente tabla para recopilar los resultados:
La siguiente tabla contiene los datos de un auto
| Tiempo (s) | Velocidad (m/s) |
| 0 | 0 |
| 5 | 60 |
| 10 | 60 |
| 15 | 60 |
| 20 | 30 |
| 25 | 30 |
| 30 | 45 |
| 35 | 27.5 |
| 40 | 10 |
| 45 | 10 |
| 50 | 10 |
| 55 | 10 |
| 60 | 0 |
Puedes bajar la gráfica en el siguiente enlace:
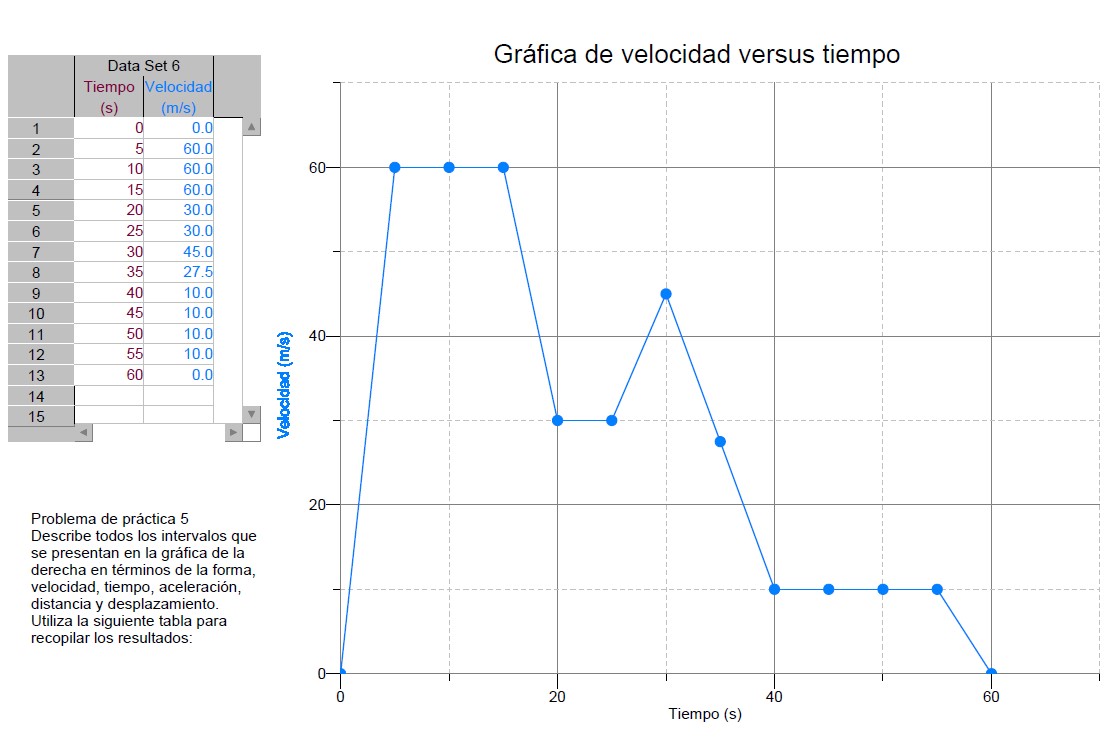
Gráfica de velocidad versus tiempo para el problema de práctica 5
Llena la tabla
Llena la siguiente tabla de acuerdo a los datos que puedes obtener de la gráfica de la derecha.
| Tramo | Forma: | Velocidad(m/s) | Tiempo (s) | Aceleración (m/s2) | Desplazamiento (m) | DesplazamientoTotal (m) |
| AB | Lineal Ascendente | Aumenta de 0 a 60m/s, NorteΔV = 60 m/s | Aumenta de 0 a 5Δt = 5 s | a=ΔV /Δt = 60m/s/5s =+12m/s2 =12m/s2, Norte | A= ½ bh = ½ (5s) (60m/s)desplazamiento=150m, Nortedistancia=150m | 150m,N |
| BC | Lineal Horizontal | Constante en 60m/s, Norte ΔV = 0 m/s | Aumenta de 5 a 15sΔt = 10 s | 0m/s2 – No hay | A= L X a = (60m/s) (10s) = 600mdesplazamiento=600m, Nortedistancia = 600m | =750m,N |
| CD | Lineal Descendente | Disminuye de 60m/s a 30m/s, NorteΔV = -30 m/s | Aumenta de 15 a 20sΔt = 5 s | a=ΔV /Δt =-30m/s/5s=-6m/s2 , Norte decelera o frena | A= ½ bh = ½ (5s) (30m/s)=75m, NorteA= L X a = (5s) (30m/s) =150m, NortePara calcular el desplazamiento sumas: 75m + 150m =Dtotal=(+225 m)= 225m, Nortedistancia = 225m | =750m+225m =975m,N |
| DE | Lineal Horizontal | Constante en 30m/s, Norte ΔV = 0 m/s | Aumenta de 20 a 25sΔt = 5 s | 0m/s2 – No hay | A= L X a = (5s) (30m/s) desplazamiento= 150m, Nortedistancia= 150m | =975m +150m=1125m,N |
| EF | Lineal Ascendente | Aumenta de 30 a 45m/s, N ΔV = 15 m/s | Aumenta de 25 a 30sΔt = 5 s | a=ΔV /Δt =15m/s/5s=+3 m/s2 =+3m/s2, Norte | A= ½ bh = ½ (5s) (15m/s)=37.5m, NorteA= L X a = (5s) (30m/s) ==150m, NortePara calcular el desplazamiento sumas: 37.5m + 150m =Dtotal=(+187.5 m)= 187.5m, Nortedistancia = 187.5m | =1125m+187.5m=1312.5m,N |
| FG | Lineal Descendente | Disminuye de 45m/s a 10m/s, Norte ΔV = -35 m/s | Aumenta de 30 a 40sΔt = 10 s | a=ΔV /Δt == -35m/s/10s-3.5 m/s2 = -3.5m/s2, Nortedecelera o frena | A= ½ bh = ½ (10s) (35m/s) ==175m, NorteA= L X a = (10s) (100m/s) =100m, NortePara calcular el desplazamiento sumas: 175m + 100m =Dtotal=(+275 m)= 275m, Nortedistancia = 275m | =1312.5m+275m=1587.5m, N |
| GH | Lineal Horizontal | Constante en 10m/s, Norte ΔV = 0 m/s | Aumenta de 40 a 55sΔt = 15 s | 0m/s2 – No hay | A= L X a = (15s) (10m/s) =desplazamiento=150m, Nortedistancia= 150m | =1587.5m+150m=1737.5m, N |
| HI | Lineal Descendente | Disminuye de 10m/s a 0m/s, Norte ΔV = -10 m/s | Aumenta de 55 a 60sΔt = 5 s | a=ΔV /Δt == -10m/s/5s-2 m/s2 = -2m/s2, Nortedecelera o frena | A= ½ bh = ½ (5s) (10m/s)desplazamiento=25m, Nortedistancia = 25m | =1737.5m+25m=1762.5m, N |
Comentarios para la tabla de datos
Observa que el objeto se mueve en todo momento hacia el norte. tiene un desplazamiento total de 1,762.5m. Cuando la gráfica es lineal ascendente demuestra un aumento en la velocidad y cuando la gráfica es lineal descendente muestra una disminución en la velocidad esto es debido a que el objeto está frenando.
Páginas asociadas a este tutorial:
<< Regresar a la Parte 1: Gráficas de velocidad vs tiempo >>
- 1 Parte 1: Gráficas de velocidad vs tiempo
- 2 Parte 2: Gráficas de velocidad vs tiempo Ejemplo 2
- 3 Parte 3: Problemas de Práctica 2 & 3 para gráficas de velocidad vs tiempo
- 4 Parte 4: Gráficas de velocidad vs tiempo – Ejemplo 3: Aceleración
- 5 Parte 5: Gráfica de velocidad vs tiempo – Problema de práctica 4
- 6 Parte 6: Gráfica de velocidad vs tiempo – Problemas de práctica 5
- 7 Parte 7: Problemas de velocidad vs tiempo Soluciones
Páginas asociadas al tema de gráficas de posición vs tiempo:
- 1 Parte 1: Introducción a Gráficas
- 2 Parte 2: Introducción a Gráficas – Ejemplo 1
- 3 Parte 3: Gráficas de posición vs tiempo
- 4 Parte 4: Gráficas de pos vs tiempo – Práctica 3
- 5 Parte 5: Solución de Problemas Posición vs Tiempo
Presentación
Enlaces externos para explorar
- Conceptos de Física: Hyperphysics
- Libros:
- NASA: Science Explorer Poster Series
- Simulaciones: PhET
- Tutorial de Física en Inglés: Physics Classroom
- Wikipedia en Español: Wikipedia
Simulación
Video
Páginas recientes
- Carl Friedrich Gauss: Matemática y Física
- La IA Revoluciona la Investigación
- Ernest Rutherford y su Legado
- Antoine Henri Becquerel y la Radiactividad
- La Ocultación en Astronomía
- Escribiendo el Póster de la Investigación
- Presentando la Investigación – Poster
- Movimiento de Traslación en el Universo
- Movimiento de Rotación en el Universo
- Webquest: Explorando el Universo
- Metodo, Procedimiento e Investigación
- Maria Skłodowska-Curie y la Radiactividad
- Investigando el Desplazamiento de Wien
- El Hielo, la Nieve y la Lluvia Helada
- Niels Bohr y la Estructura Atómica
- Stephen Hawkings: Pionero de Física
- Alessandro Volta y la Electricidad
- Momento Angular: Relación con el Torque
- Carl Sagan: Un Visionario
- Fondo de Radiación Cósmica
- El Misterioso Impulsor del Universo
- La Velocidad de las Gotitas de Lluvia
- Cúmulos Estelares en el Espacio
- Los Vectores y la Solución Física
- Energía y Fuerza el Dúo Dinámico
- Una Nebulosa es Polvo y Gas
- La Física de la Lluvia: Fuerzas y Más
- Ley de Avogadro y los Gases
- Rotación de las Galaxias
- La Energía que Acelera el Universo
Más para explorar
-
Herramientas para el Análisis Gráfico

Para que una gráfica sea útil, esta debe ser dibujada adecuadamente. Las gráficas permiten una visualización inmediata de los datos.
-
Los Estados de la Materia
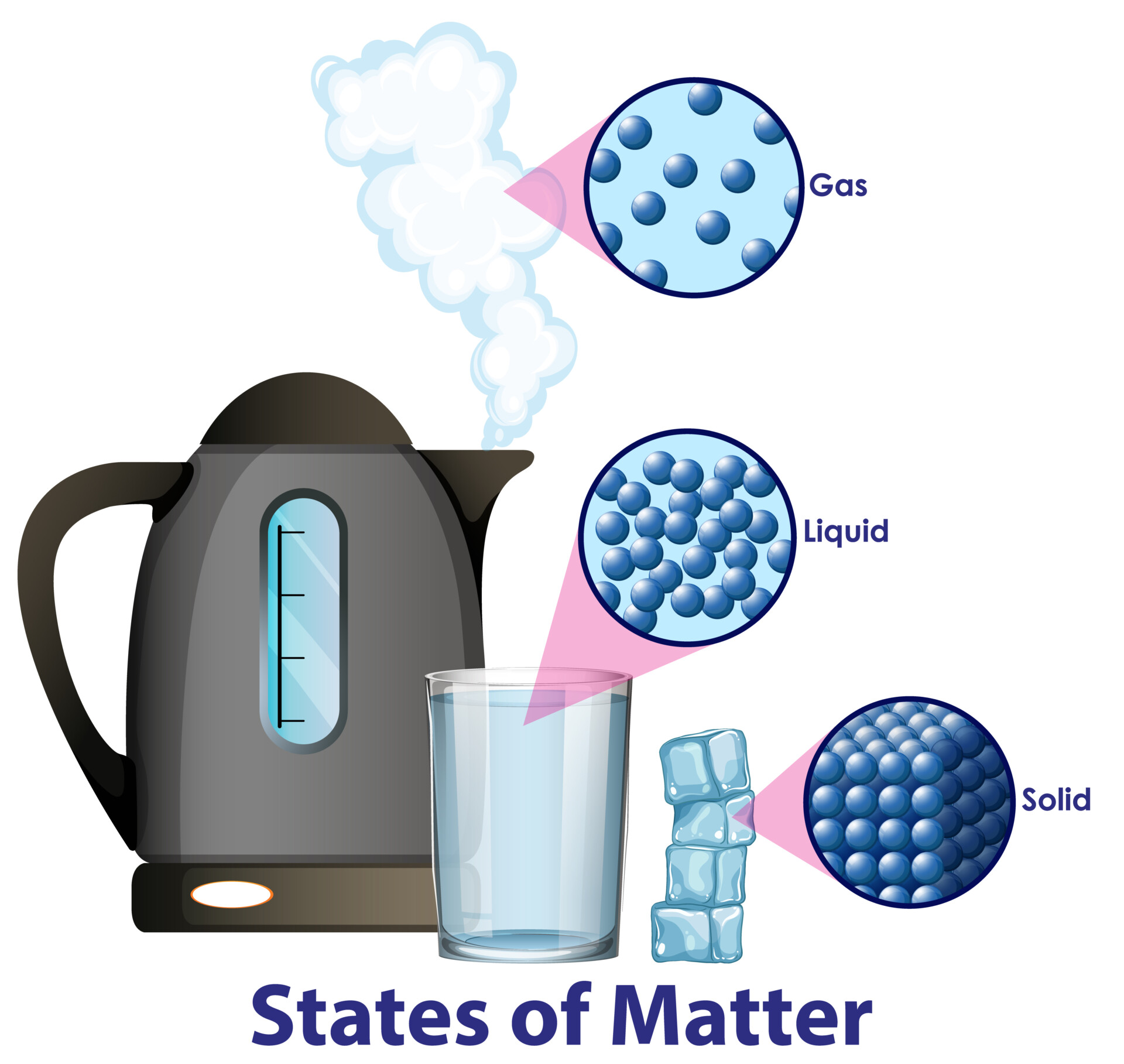
Los estados de la materia son formas de la materia en el universo. Se distinguen porque sus partículas constituyentes (átomos, moléculas o iones) se agrupan.
-
Compara Balanzas: Análoga o Digital
La balanza es una palanca de primer grado que tiene dos brazos de igual tamaño, Mediante el equilibrio entre los pesos de dos cuerpos comparas sus masas.
-
Mecánica Clásica y Análisis Gráfico

La mecánica clásica, como ya hemos visto, se encarga de estudiar el movimiento de los cuerpos y las fuerzas que lo causan.
-
Herramientas Para Medir la Masa

La balanza es una palanca de primer grado que tiene dos brazos de igual tamaño, Mediante el equilibrio entre los pesos de dos cuerpos comparas sus masas.
-
La Física y las Gráficas de Velocidad
Una gráfica de velocidad vs. tiempo es una representación visual de cómo cambia la velocidad de un objeto a lo largo del tiempo.
-
Trigonometría: Un Mundo de Ángulos

La trigonometría es una rama de las matemáticas que se dedica al estudio de las relaciones entre los lados y los ángulos de los triángulos.
-
Sumar y Restar con Cifras Significativas

Los dígitos significativos aportan información real sobre la precisión de una medida. Nos indican qué tan confiables son los números que estamos utilizando.
-
Un Viaje Vectorial por la Física
Webquest: Exploraremos el mundo de los vectores, desde su definición hasta sus aplicaciones en física que incluye el movimiento, las fuerzas y los campos.
-
El Dinamómetro: Midiendo Fuerzas
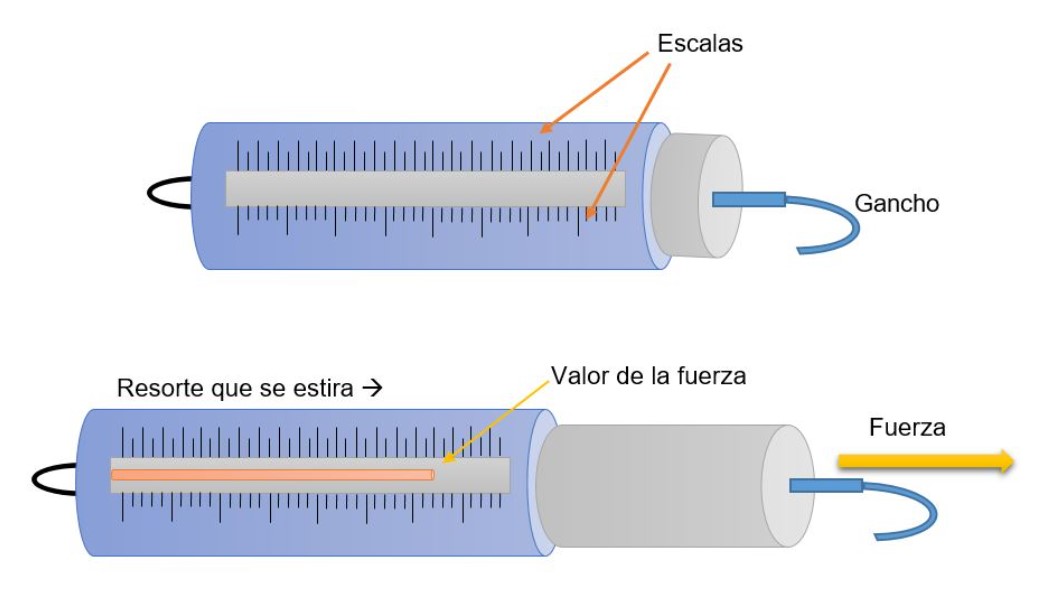
Un dinamómetro es un instrumento utilizado para medir fuerzas. Fue inventado por Isaac Newton y no debe confundirse con la balanza.
-
Vectores en Física: Guía Básica

un vector es una magnitud que, además de tener un valor numérico (magnitud), posee una dirección y un sentido. Nos indica la dirección o sentido y cuánto es.
-
Movimiento Rectilíneo: Trayectoria Recta

El movimiento rectilíneo es en el que un objeto se desplaza siguiendo una trayectoria recta, por lo tanto se mueve siempre en la misma dirección y sentido.
-
Porciento de Error en una Medida

El porcentaje de error es una medida que nos indica cuán precisa es una medición en comparación con un valor real o aceptado como correcto
-
Los M&M y la Notación Científica

En este Webquest, descubrirás cómo la notación científica, está presentes en los M&M que utilizaremos para calcular el porciento, y la probabilidad.
-
Velocidad Terminal y Resistencia

La velocidad terminal es la velocidad máxima constante que alcanza un objeto que cae a través de un fluido, igualando la fuerza de rozamiento a su peso.
-
Fuerza de Tensión en una Soga

La tensión es una fuerza de interacción que ocurre en dos direcciones; cuando halas o empujas un cuerpo con una cuerda, un resorte o un material.
-
Leyes de Movimiento Planetario de Kepler

Johannes Kepler (1571-1630), fue astrónomo y filósofo alemán. Formuló y verificó las tres leyes del movimiento planetario conocidas como leyes de Kepler.
-
Vectores en dos Dimensiones

Un vector en dos dimensiones es una entidad matemática que posee magnitud (longitud) como dirección en un plano. Los componentes se son un par ordenado.
-
Segunda Ley de Newton: Ley de la Dinámica

La aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre él e inversamente proporcional a su masa.
-
Origen de Coordenadas o Referencia

El origen de coordenadas también se conoce como el punto de referencia o de aplicación de un sistema de coordenadas. Es el comienzo al dibujar vectores.
-
Vectores en una Dimensión

La suma de vectores es un proceso matemático que utiliza el método gráfico y el método matemático para obtener un vector resultante con magnitud y dirección.
-
Introducción a la Cinemática y Movimiento

La cinemática es la rama de la física que se encarga de describir el movimiento de los objetos, sin considerar las causas que lo producen.
-
Rapidez, Velocidad y Marco de Referencia

El movimiento ocurre continuamente debido al cambio continuo en la posición de un objeto que sugiere que puede haber un movimiento.
-
La gravedad y la relatividad general

Todos los objetos son atraídos hacia la Tierra. La fuerza ejercida por la Tierra sobre los objetos se denomina fuerza de gravedad.
-
Introducción a Gráficas

La mecánica clásica describe el movimiento de los objetos en términos del espacio y el tiempo, sin tomar en cuenta los agentes que lo producen.
-
La Fuerza Aplicada y la Fuerza de Empuje

La fuerza aplicada es un término general dado a las fuerzas externas que actúan directamente sobre un cuerpo y lo mueven.
-
Distancia y Desplazamiento: Su Significado

Los términos distancia y desplazamiento se utilizan como sinónimos, aunque en realidad tienen un significado diferente. Distancia es la cantidad movida.
-
Gráfica de v vs t – Práctica 2 & 3
Describe los intervalos de la tabla que de acuerdo con la gráfica que dibujarás y que debe tener marcados solamente cuatro puntos: A, B, C y D.
-
Rapidez y Velocidad: No es lo mismo!

Los conceptos distancia y desplazamiento ayudan en la descripción del movimiento, sin embargo la rapidez y la velocidad no son lo mismo.
-
Aceleración en Caída Libre

La aceleración es la razón de cambio en la velocidad de un objeto respecto al tiempo. La aceleración se refiere a cuan rápido un objeto cambia su velocidad.