
Objetivos:
Al terminar esta lección:
- Definirás los conceptos: rapidez y velocidad.
- Diferenciarás entre lo que es rapidez y velocidad.
- Calcularás la rapidez y la velocidad promedio de un objeto.
Introducción
Los conceptos distancia y desplazamiento ayudan en la descripción del movimiento. En nuestra vida diaria a veces utilizamos los conceptos de rapidez o velocidad como si fueran lo mismo, en realidad no son lo mismo aunque tienen cierto parecido. En esta página proveemos ejemplos de los conceptos de rapidez y velocidad.
Movimiento con rapidez o velocidad constante
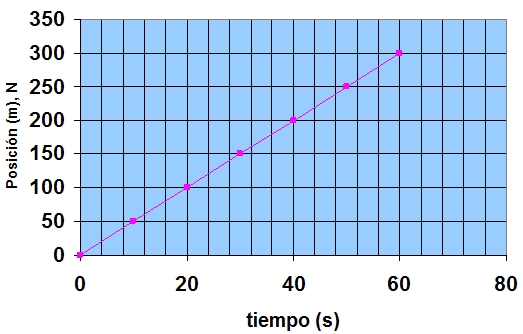
Cuando la rapidez de un objeto es constante se mantiene viajando uniformemente. Considera la siguiente gráfica:
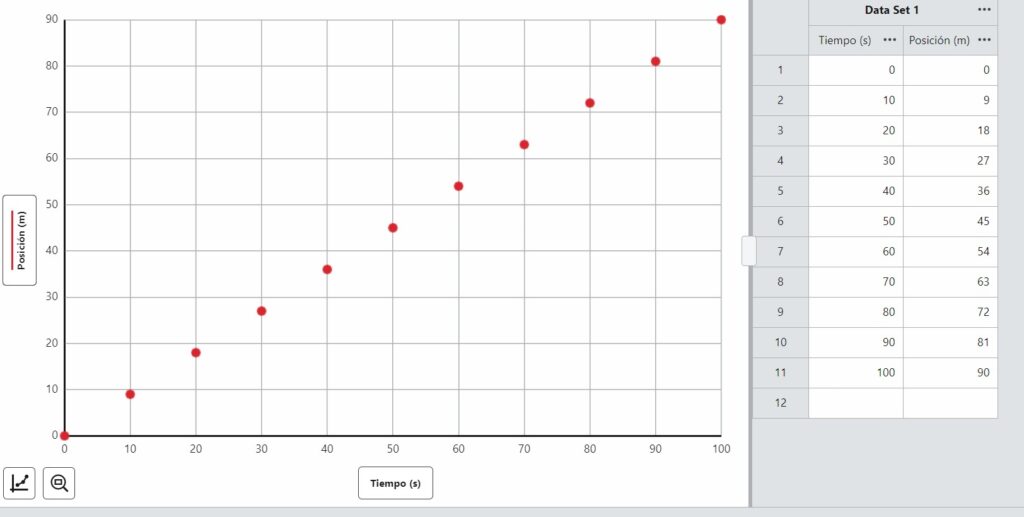
Ecuación
El objeto recorre una distancia de nueve metros en diez segundos. Sin embargo, la segunda gráfica aquí abajo presenta un objeto con rapidez variable.
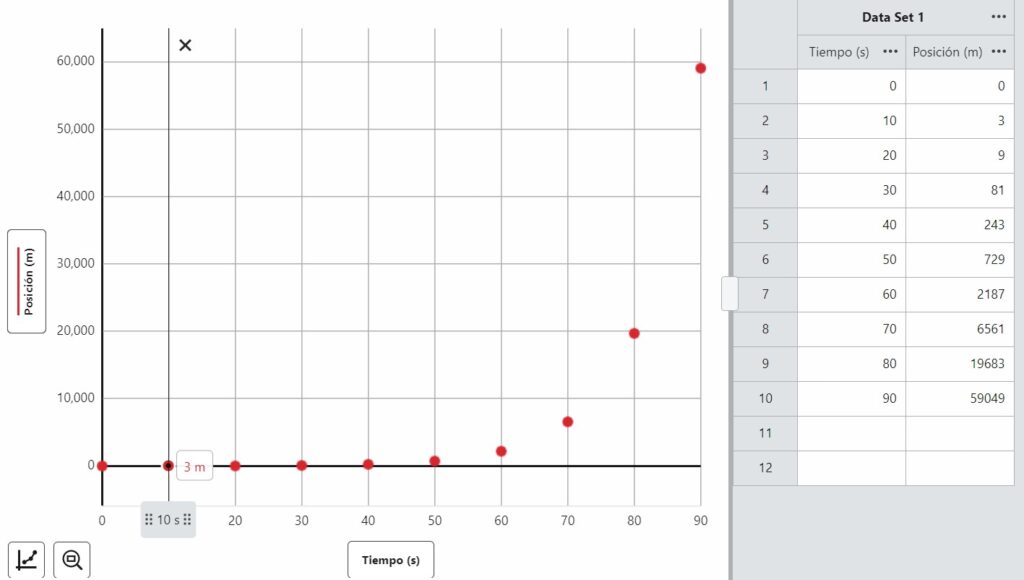

Al principio el mismo viajaba lentamente y más rápido al final. Esto lo sabemos al observar que el cambio en la posición por cada segundo que transcurre es cada vez mayor. Al hablar de la rapidez en este segundo caso, tenemos que hablar de la rapidez promedio. Matemáticamente se define la rapidez como:
v = d/t
Discusión del ejemplo
Donde d es la distancia y t es el tiempo. En el caso de nuestro objeto en ambos casos la rapidez promedio es de 0.9 m/s (3.24 km/hr). Si durante el recorrido del primer caso, observarás el velocímetro del objeto, notarías que el mismo estaría marcando 0.9 m/s todo el tiempo.
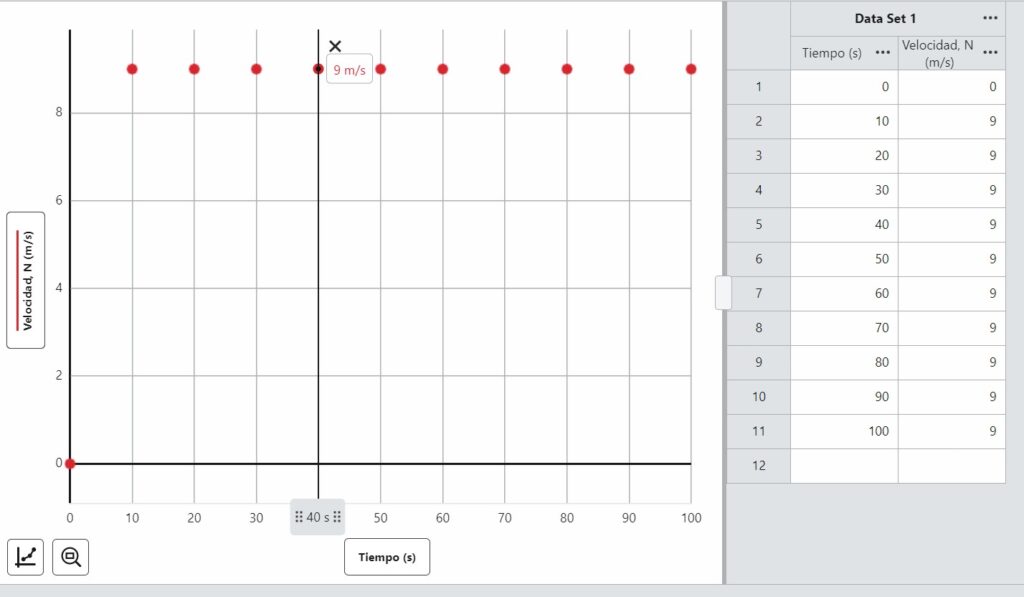
Sin embargo en el caso que discutimos, observarías como el velocímetro se mantiene cada instante en una velocidad similar, siendo el promedio de las lecturas 0.9 m/s. Sin embargo, la rapidez en cualquier instante, se conoce como la rapidez instantánea. La rapidez instantánea de un objeto, es la rapidez con la que el objeto se mueve en un instante dado. Puedes observar los instantes marcados en rojo en la gráfica. Si el objeto se moviera exactamente la misma distancia por cada unidad de tiempo, entonces la rapidez sería constante, por lo que la rapidez instantánea sería igual a la rapidez promedio.

La velocidad es una cantidad vectorial
Otro concepto que podemos utilizar para describir el movimiento de un objeto es la velocidad (v). La velocidad es una cantidad vectorial, por lo que requiere de una magnitud con sus unidades de medida y una dirección para referirnos a ella. La magnitud de la velocidad es la rapidez del objeto. Al igual que la rapidez, también nos referimos a la velocidad como velocidad promedio. La velocidad promedio se puede calcular a partir de la ecuación:
v = d/t
En este caso, d es el desplazamiento, mientras t es el tiempo. Utilizamos letras en negritas para las cantidades vectoriales. Por tal motivo: v es la rapidez mientras que v es la velocidad.
Ejemplo 1:
A un tren, le toma 2.0 horas en viajar entre las ciudades de París y Lion que se encuentra a 454.0 km hacia el sur. ¿Cuál es la velocidad promedio del tren?
Dado:
- Desplazamiento, d= 454 km, sur
- Tiempo, t= 2.0 horas
- Velocidad promedio, v= ?
Ecuación:
v = d / t
Solución:
v = d / t
= 454 km / 2 h
= 227 km/h, sur
Respuesta:
- La velocidad fue de 227 km/h en dirección sur.
Desplazamiento y tiempo
Un objeto que se mueve con velocidad constante tendrá un desplazamiento igual durante cada segundo de movimiento. Así que el desplazamiento será proporcional al tiempo, siendo la velocidad la constante de proporción. Si la velocidad aumenta, el desplazamiento por segundo será mayor. La ecuación que describe esta relación es:
d = vt
Es una ecuación lineal
Fíjate que esta ecuación está escrita de la forma y = mx + b. Esta es la ecuación que describe las gráficas lineales, donde m es la pendiente y b el intercepto en el eje de y. La pendiente se refiere a la inclinación de la gráfica y la llamamos constante de proporción. Indica cuanto cambia la y por cada cambio en x. El intercepto en el eje de y indica el valor de y cuando la x es igual a cero.
La gráfica de posición versus tiempo para un objeto que se mueve con velocidad constante será una línea recta. Como la pendiente de una gráfica lineal indica el cambio en la posición respecto al cambio en el tiempo, entonces la pendiente de la gráfica es la velocidad.
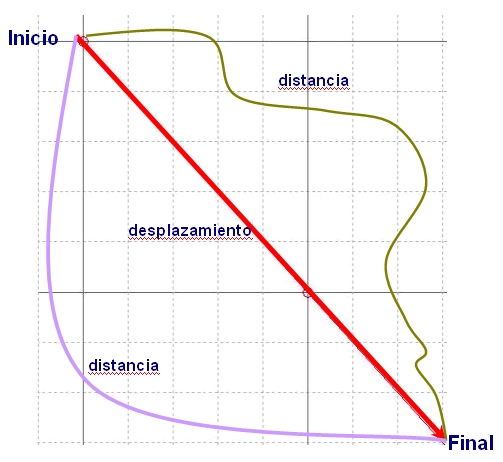
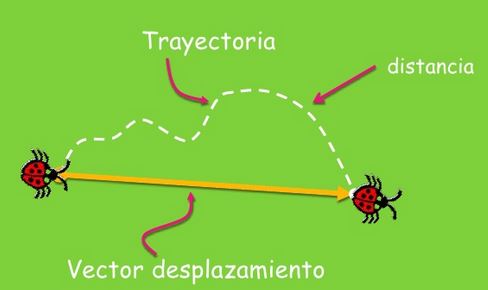
La trayectoria
La rapidez depende de la trayectoria y de la distancia recorrida. Mientras que la velocidad depende del desplazamiento el cual solo considera el punto de comienzo y el punto final del evento. La próxima imagen muestra la diferencia entre distancia y desplazamiento.
Páginas relacionadas a este tema
- Aceleración Lineal y sus Representaciones
- Análisis Gráfico del Movimiento
- Introducción a Gráficas
- Marco de Referencia y Movimiento
- Origen de Coordenadas o Referencia
- Rapidez, Velocidad y Marco de Referencia
- Rapidez y velocidad: ¡No es lo mismo!
- Sistema de Coordenadas en Física
- Vectores en una Dimensión
- Vectores en dos Dimensiones
Enlaces externos para explorar
- Conceptos de Física: Hyperphysics
- Libros:
- NASA: Science Explorer Poster Series
- Simulaciones: PhET
- Tutorial de Física en Inglés: Physics Classroom
- Wikipedia en Español: Wikipedia
Simulación
Vídeo
Páginas recientes
- Carl Friedrich Gauss: Matemática y Física

- La IA Revoluciona la Investigación

- Ernest Rutherford y su Legado

- Antoine Henri Becquerel y la Radiactividad

- La Ocultación en Astronomía

- Escribiendo el Póster de la Investigación

- Presentando la Investigación – Poster

- Movimiento de Traslación en el Universo

- Movimiento de Rotación en el Universo

- Webquest: Explorando el Universo

- Metodo, Procedimiento e Investigación

- Maria Skłodowska-Curie y la Radiactividad
- Investigando el Desplazamiento de Wien

- El Hielo, la Nieve y la Lluvia Helada

- Niels Bohr y la Estructura Atómica
Más páginas para explorar
-
Microgravedad en la Luna
En la Luna, lo que experimentan los astronautas y los objetos no es una ausencia total de gravedad, sino microgravedad, o más precisamente, baja gravedad.
-
Herramientas para el Análisis Gráfico

Para que una gráfica sea útil, esta debe ser dibujada adecuadamente. Las gráficas permiten una visualización inmediata de los datos.
-
Proyectil, Balística y Física

Un proyectil es un objeto lanzado cuya fuerza que actúa es la gravitacional. Este puede ser un balón de baloncesto, de fútbol una flecha o una bala de cañón.
-
Los Estados de la Materia
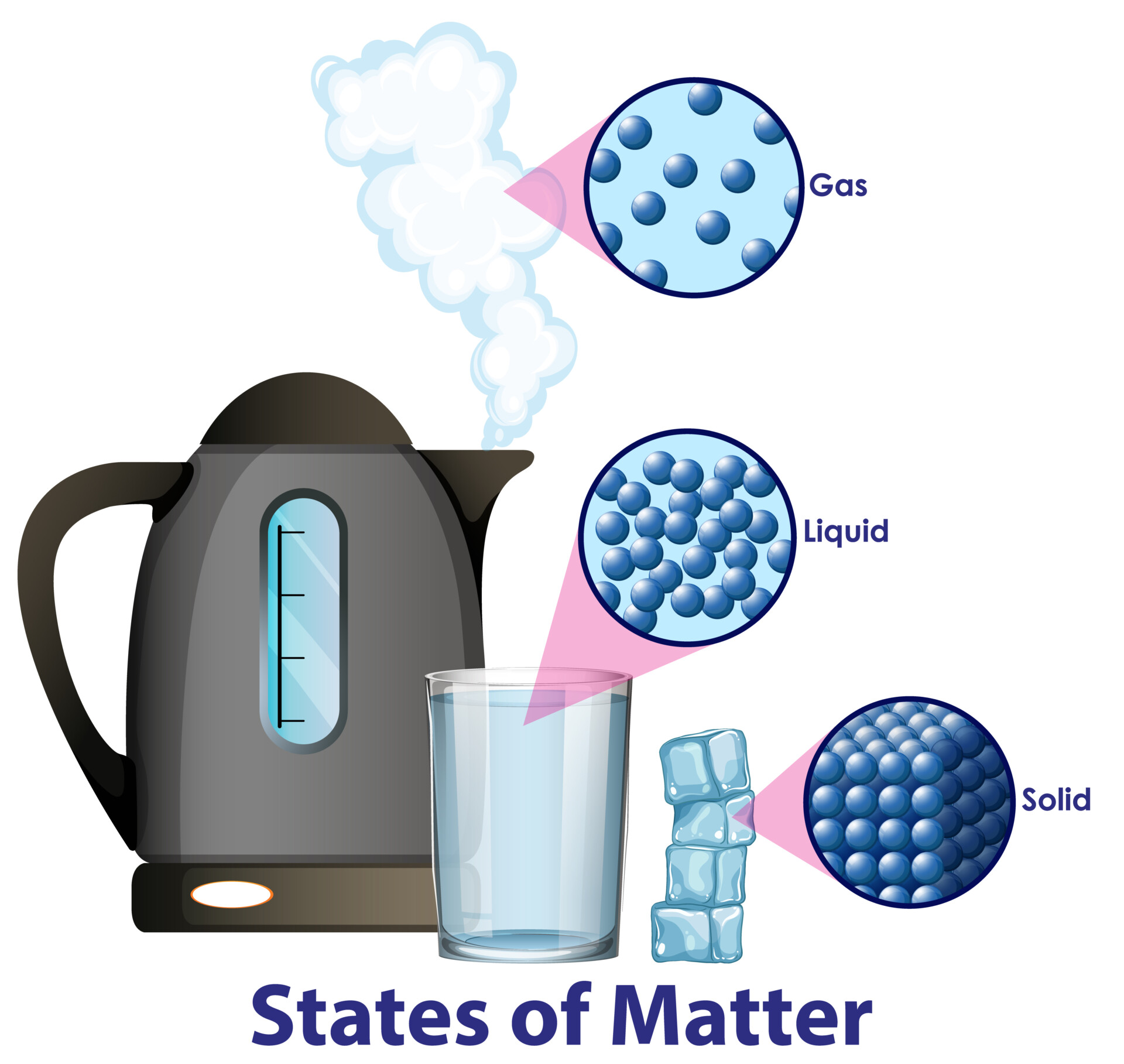
Los estados de la materia son formas de la materia en el universo. Se distinguen porque sus partículas constituyentes (átomos, moléculas o iones) se agrupan.
-
Mecánica Clásica y Análisis Gráfico

La mecánica clásica, como ya hemos visto, se encarga de estudiar el movimiento de los cuerpos y las fuerzas que lo causan.
-
La Física y las Gráficas de Velocidad
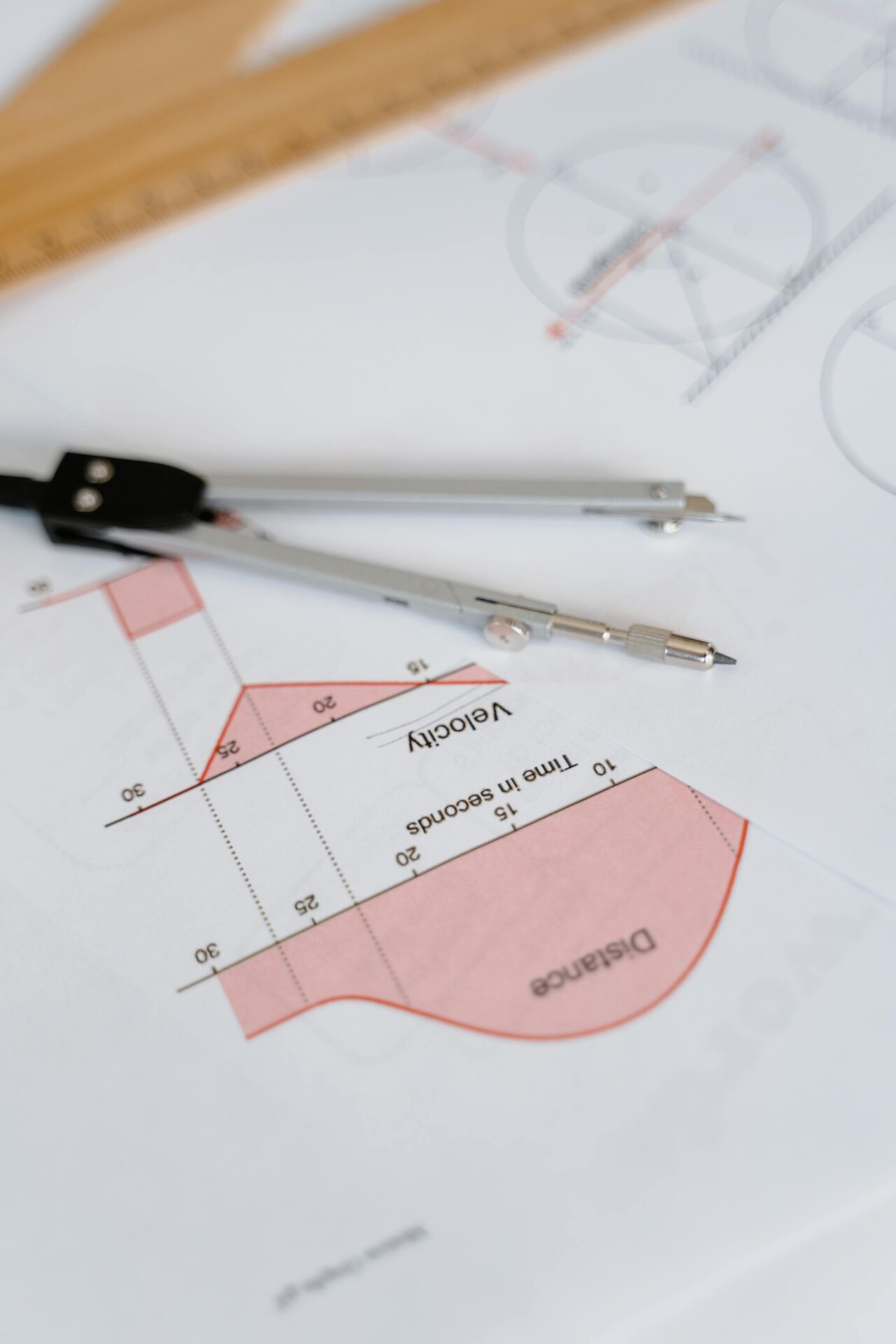
Una gráfica de velocidad vs. tiempo es una representación visual de cómo cambia la velocidad de un objeto a lo largo del tiempo.
-
Temperatura: Una Medida de Energía

La temperatura es una propiedad física e intensiva de la materia que no depende de la cantidad de materia ni promueve el cambio estructural de la misma.
-
Un Viaje Vectorial por la Física
Webquest: Exploraremos el mundo de los vectores, desde su definición hasta sus aplicaciones en física que incluye el movimiento, las fuerzas y los campos.
-
El Dinamómetro: Midiendo Fuerzas
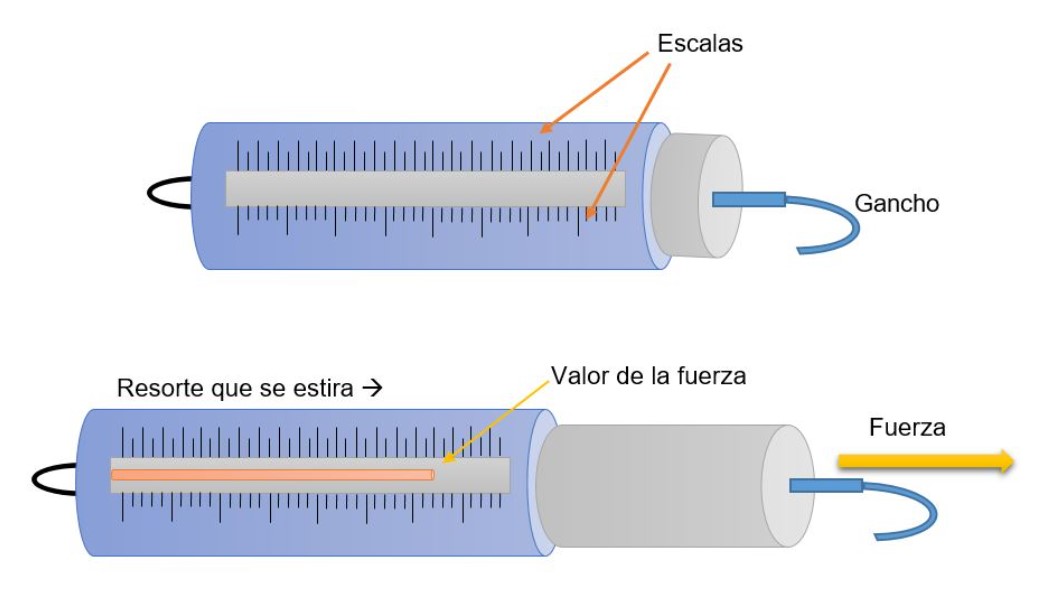
Un dinamómetro es un instrumento utilizado para medir fuerzas. Fue inventado por Isaac Newton y no debe confundirse con la balanza.
-
Sistema Internacional Unidades y Ciencia

El Sistema Internacional de Unidades, comúnmente abreviado como SI, es un sistema de medidas que se utiliza como referencia en casi todos los países del mundo.
-
La Fricción Resiste el Movimiento

La fricción es una fuerza paralela de contacto que actúa al oponerse al movimiento deslizante entre las superficies en contacto.
-
Volumen: Una Medida de Espacio

El volumen, magnitud física para midir el espacio tridimensional ocupado por un objeto o sustancia. Se cuantifica por el largo, ancho y alto.
-
Vectores en Física: Guía Básica

un vector es una magnitud que, además de tener un valor numérico (magnitud), posee una dirección y un sentido. Nos indica la dirección o sentido y cuánto es.
-
Porciento de Error en una Medida

El porcentaje de error es una medida que nos indica cuán precisa es una medición en comparación con un valor real o aceptado como correcto
-
Proyectil es Energía Cinética y Potencial

Un proyectil es un objeto lanzado cuya fuerza que actúa es la gravitacional. Este puede ser un balón de baloncesto, de fútbol una flecha o una bala de cañón.
-
Micrómetro: Instrumento de Precisión

Micrometro, una herramienta para medir objetos pequeños. Este tipo de escala de micrómetro también es conocido como calibre.
-
Fuerza de Tensión en una Soga

La tensión es una fuerza de interacción que ocurre en dos direcciones; cuando halas o empujas un cuerpo con una cuerda, un resorte o un material.
-
Leyes de Movimiento Planetario de Kepler

Johannes Kepler (1571-1630), fue astrónomo y filósofo alemán. Formuló y verificó las tres leyes del movimiento planetario conocidas como leyes de Kepler.
-
Johannes Kepler y sus Leyes

Johannes Kepler (1571-1630), fue astrónomo y filósofo alemán. Formuló y verificó las tres leyes del movimiento planetario conocidas como leyes de Kepler.
-
Momentum: Cantidad Fundamental

El momentum es cantidad de movimiento. Se estudia para saber como se comportan los cuerpos en interacción en las colisiones.
-
Volumen: Una Cantidad Tridimensional

El volumen, magnitud física para midir el espacio tridimensional ocupado por un objeto o sustancia. Se cuantifica por el largo, ancho y alto.
