Trigonometría y el Teorema de Pitágoras

Objetivos

Al terminar esta lección:

• Definirás las funciones trigonométricas a partir de la geometría del triángulo rectángulo.
• Utilizarás las funciones trigonométricas para hallar las medidas desconocidas de un triángulo rectángulo.
• Seleccionarás correctamente la función trigonométrica apropiada para resolver los problemas.

---

La Trigonometría 

La trigonometría es el estudio de las relaciones entre los lados y los ángulos de un triángulo por las funciones trigonométricas de los ángulos. Estas son: seno, coseno y tangente. Las funciones trigonométricas se pueden definir por las relaciones entre los lados y los ángulos de un triángulo rectángulo.

Triángulo de ejemplo

Si llamamos a a uno de los lados del triángulo rectángulo, A es el punto del vértice opuesto a a y b es el lado opuesto a B y es el lado adyacente a a y C por ser opuesto al ángulo recto (90°) es la hipotenusa, entonces las funciones trigonométricas de los triángulos rectángulos quedan definidas así:

• Sen θ= lado opuesto / hipotenusa = A/C
• Cos θ= lado adyacente / hipotenusa = B/C
• Tan θ= lado opuesto / lado adyacente = A/B

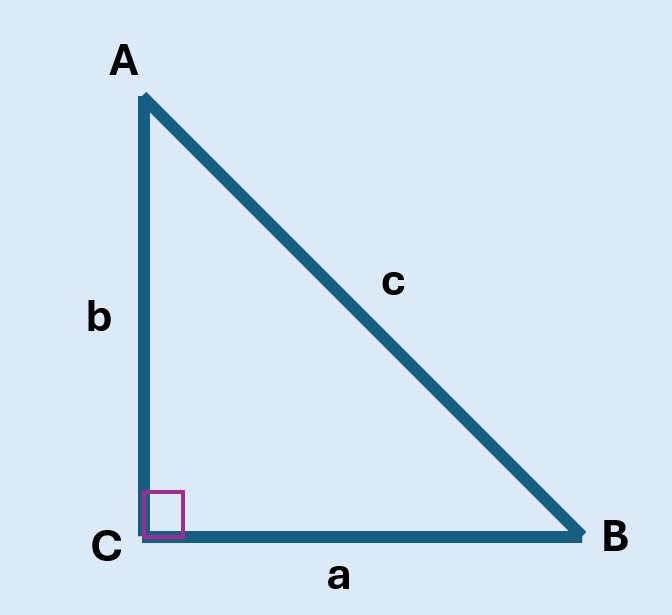
Los triángulos son figuras de tres lados

Los triángulos rectángulos son figuras geométricas de tres lados y tres ángulos. Uno de sus ángulos mide 90°. Esto significa que es un ángulo recto. Como todos los triángulos planos, la suma de sus ángulos es igual a 180°. En términos de sus lados, el triángulo rectángulo siempre tiene un lado de mayor longitud. A este lado se le denomina la hipotenusa. La hipotenusa es el lado opuesto al ángulo de 90° o ángulo recto.

El teorema de Pitágoras 

Los lados de un triángulo rectángulo se pueden relacionar entre sí por medio del teorema de Pitágoras.  La ecuación que describe esa relación es la siguiente:

c² = a² + b²

No importa el tamaño del triángulo,  la proporción existente entre los lados, a partir de un ángulo de referencia, se mantiene constante.  Esto significa que si dibujas dos triángulos rectángulos de diferente tamaño con uno de sus ángulos iguales verás que hay una similitud.  Mide los lados de cada triángulo y establece la proporción para cada lado según se definen las funciones trigonométricas y verás que las proporciones entre los dos triángulos se mantiene independientemente del tamaño del triángulo.

Ejemplo 1: Triángulo ABC

Sea ABC un triángulo rectángulo con lados a, b y c, como muestra la figura.

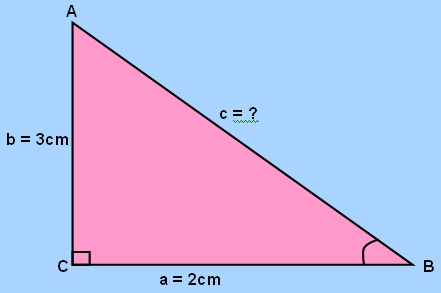
Si el lado c es la hipotenusa, entonces:

c² = a² + b²

Si el cateto a = 2 cm y el cateto b = 3 cm, entonces

c² = a² + b²

c² = (2 cm) ² + ( 3 cm)²

c² = 4 cm² + 9 cm²

c² = 13 cm²

c = 3.6 cm

•  La medida del lado c es de 3.6 cm.

---

Tarea adicional para la aplicación de conceptos

Si quieres aprender un poco más sobre el Teorema de Pitágoras, puedes contestar las siguientes preguntas:

1. ¿Quén descubrió el Teorema de Pitágoras?
2. ¿De qué se trata el Chou Pei?  ¿Por qué fue importante?
3. ¿Qué aplicaciones puede tener el Teorema?
4. Utiliza los siguientes enlaces para que puedas buscar información adicional que te ayudará a responder las preguntas.

• Wikipedia
• Curso de Física universitaria

---

Simulación

Vector Addition

---

Enlaces externos para explorar

• Conceptos de Física: Hyperphysics
• Libros:
  • Física Moderna de Paul A. Tipler
  • Física Moderna – Raymond A. Serway
• NASA: Science Explorer Poster Series
• Simulaciones: PhET
• Tutorial de Física en Inglés: Physics Classroom
• Wikipedia en Español: Wikipedia

---

Información básica sobre la trigonometría

Este video explica la historia y ejemplos básicos sobre la trigonometría.

---

Páginas recientes

• 
  Webquest es una Aventura en Línea
• 
  Vúmetro y la Amplitud del Sonido
• 
  Volumen: Una Cantidad Tridimensional
• 
  Vernier: Herramienta Muy Versátil
• 
  Velocidad Terminal y Resistencia
• 
  Vectores: Cantidad y Dirección
• 
  Vectores en una Dimensión
• 
  Vectores en dos Dimensiones
• 
  Universo es Todo lo que Existe
• 
  Unidades Fundamentales en Ciencia
• 
  Tycho Brahe: Astronomía y Observación
• 
  Trigonometría y el Teorema de Pitágoras
• 
  Trigonometría Básica Ilustrada
• 
  Trabajo y la transferencia de energía
• 
  Torque: El Momento de Fuerza
• 
  Título de la Investigación
• 
  Tipos de Errores Experimentales
• 
  Tiempo es una Ilusión que Existe
• 
  Tiempo de Reacción al Frenar
• 
  Termodinámica
• 
  Tercera Ley de Newton es Fundamental
• 
  Temperatura una Propiedad Física
• 
  Telescopio Reflector Newtoniano
• 
  Técnicas Para Estudiar las Estrellas
• 
  Superconductores
• 
  Stonehenge: Un Ministerio Astronómico
• 
  Sonido
• 
  Solución de Problemas Posición vs Tiempo
• 
  Sistema Internacional de Medidas: Recursos
• 
  Sistema de Posicionamiento Global es GPS

---

Más páginas para explorar

---

Para explorar